题目内容
(本题满分16分)本题共有2个小题,第1小题满分8分,第2小题满分8分.
已知双曲线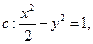 设过点
设过点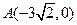 的直线l的方向向量
的直线l的方向向量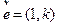
(1) 当直线l与双曲线C的一条渐近线m平行时,求直线l的方程及l与m的距离;
(2) 证明:当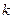 >
>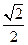 时,在双曲线C的右支上不存在点Q,使之到直线l的距离为
时,在双曲线C的右支上不存在点Q,使之到直线l的距离为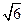 .
.
已知双曲线
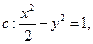 设过点
设过点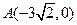 的直线l的方向向量
的直线l的方向向量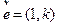
(1) 当直线l与双曲线C的一条渐近线m平行时,求直线l的方程及l与m的距离;
(2) 证明:当
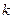 >
>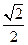 时,在双曲线C的右支上不存在点Q,使之到直线l的距离为
时,在双曲线C的右支上不存在点Q,使之到直线l的距离为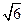 .
.(1)双曲线C的渐近线 ,即
,即 …… 2分
…… 2分
 直线
直线 的方程
的方程 …… 6分
…… 6分
 直线
直线 与m的距离
与m的距离 …… 8分
…… 8分
(2) 设过原点且平行于
设过原点且平行于 的直线
的直线
则直线 与
与 的距离
的距离
 ,
,
当 时,
时, . …… 12分
. …… 12分
又双曲线C的渐近线为 ,
,
 双曲线C的右支在直线
双曲线C的右支在直线 的右下方,
的右下方,
 双曲线C的右支上的任意点到直线
双曲线C的右支上的任意点到直线 的距离大于
的距离大于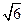 .
.
故在双曲线C的右支上不存在点Q 到到直线
到到直线 的距离为
的距离为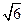 …… 16分
…… 16分
 假设双曲线C右支上存在点Q
假设双曲线C右支上存在点Q 到到直线
到到直线 的距离为
的距离为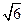 ,
,
则 , (1)由(1)得
, (1)由(1)得 , …… 11分
, …… 11分
设
当 时,
时, :
:
 …… 13分
…… 13分
将 代入(2)得
代入(2)得 ,
,

 ,
,


故在双曲线C的右支上不存在点Q 到到直线
到到直线 的距离为
的距离为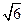 …… 16分
…… 16分
 ,即
,即 …… 2分
…… 2分 直线
直线 的方程
的方程 …… 6分
…… 6分 直线
直线 与m的距离
与m的距离 …… 8分
…… 8分(2)
 设过原点且平行于
设过原点且平行于 的直线
的直线
则直线
 与
与 的距离
的距离
 ,
,当
 时,
时, . …… 12分
. …… 12分又双曲线C的渐近线为
 ,
, 双曲线C的右支在直线
双曲线C的右支在直线 的右下方,
的右下方, 双曲线C的右支上的任意点到直线
双曲线C的右支上的任意点到直线 的距离大于
的距离大于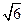 .
. 故在双曲线C的右支上不存在点Q
 到到直线
到到直线 的距离为
的距离为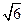 …… 16分
…… 16分 假设双曲线C右支上存在点Q
假设双曲线C右支上存在点Q 到到直线
到到直线 的距离为
的距离为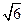 ,
,
|
 , (1)由(1)得
, (1)由(1)得 , …… 11分
, …… 11分设

当
 时,
时, :
: …… 13分
…… 13分将
 代入(2)得
代入(2)得 ,
,
 ,
,


故在双曲线C的右支上不存在点Q
 到到直线
到到直线 的距离为
的距离为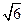 …… 16分
…… 16分⑴中知道双曲线的方程可以求出渐近线方程,因为直线l和渐近线平行,所以可以确定l的方程,直线l与m方程确定,可以利用两条平行线间的距离公式求出距离.⑵是一个存在性问题,可以寻找参考对象,也可用反证法.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 ,它的离心率为
,它的离心率为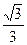 ,直线
,直线 与以原点为圆心,以椭圆
与以原点为圆心,以椭圆 的短半轴长为半径的圆相切.⑴求椭圆
的短半轴长为半径的圆相切.⑴求椭圆 ,左准线为
,左准线为 ,动直线
,动直线 垂直于直线
垂直于直线 ,线段
,线段 的垂直平分线交
的垂直平分线交 ,求动点
,求动点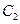 的方程;⑶将曲线
的方程;⑶将曲线 ,设曲线
,设曲线 ,焦点为
,焦点为 ,过
,过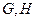 两点,过点
两点,过点 作平行于曲线
作平行于曲线 ,若
,若 ,试证明三点
,试证明三点 (
( 为坐标原点)在同一条直线上.
为坐标原点)在同一条直线上.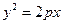 的焦点与椭圆
的焦点与椭圆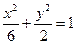 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( )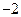
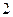


 ,点
,点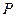 满足
满足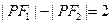 ,记点
,记点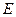 .
.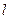 过点
过点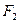 且与轨迹
且与轨迹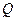 两点. (i)设点
两点. (i)设点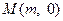 ,问:是否存在实数
,问:是否存在实数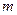 ,使得直线
,使得直线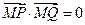 成立?若存在,求出实数
成立?若存在,求出实数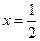 的垂线
的垂线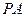 、
、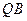 ,垂足分别为
,垂足分别为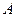 、
、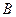 ,记
,记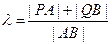 ,求
,求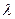 的取值范围.
的取值范围. 上任意一点到两焦点距离之和为4,直线
上任意一点到两焦点距离之和为4,直线 为该椭圆的一条准线.
为该椭圆的一条准线. 与椭圆C交于不同的两点
与椭圆C交于不同的两点 且
且 (其中
(其中 为坐标原点),求直线
为坐标原点),求直线 的斜率
的斜率 的取值范围.
的取值范围. 的焦点与椭圆
的焦点与椭圆 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( )