题目内容
已知双曲线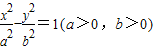 的右准线l2与一条渐近线l交于点P,F是双曲线的右焦点.
的右准线l2与一条渐近线l交于点P,F是双曲线的右焦点.(Ⅰ)求证:PF⊥l;
(Ⅱ)若
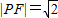 ,且双曲线的离心率
,且双曲线的离心率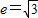 ,求该双曲线的方程;
,求该双曲线的方程;(Ⅲ)若过点A(2,1)的直线与(Ⅱ)中的双曲线交于两点P1,P2,求线段P1P2的中点M的轨迹方程.
【答案】分析:(Ⅰ)由双曲线方程求出双曲线的右准线方程和一条渐近线方程,联立求出P点的坐标,求出PF所在直线的斜率,由斜率制剂等于-1证明PF⊥l;
(Ⅱ)由(Ⅰ)中的证明可知,|PF|为F(c,0)到l:bx-ay=0距离,由点到直线的距离公式列一个关于a,b,c的关系式,再由离心率得一关系式,结合a2+b2=c2求解a,b的值,则双曲线的方程可求;
(Ⅲ)分斜率存在和不存在得到过点A的直线方程,斜率存在时把直线方程和双曲线方程联立,利用根与系数关系得到M点的参数方程,消参后即可得到答案,然后验证斜率不存在时的情况.
解答:(Ⅰ)证明:右准线为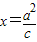 ,由对称性,不妨设渐近线l为
,由对称性,不妨设渐近线l为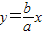 ,则
,则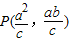 .
.
又F(c,0),∴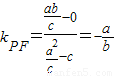 .
.
又∵ ,∴
,∴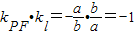 ,∴PF⊥l;
,∴PF⊥l;
(Ⅱ)解:∵|PF|为F(c,0)到l:bx-ay=0距离,∴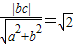 ,即b=
,即b=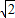 .
.
又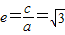 ,∴
,∴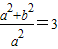 ,解得a2=1.
,解得a2=1.
故双曲线方程为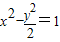 ;
;
(Ⅲ)解:设M(x,y),
当过点A的直线斜率存在时,设直线方程为y-1=k(x-2),
由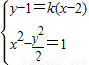 ,
,
可得(2-k2)x2-2k(1-2k)x-(1-2k)2-2=0.
当(2-k2)≠0,△=(1-2k)24k2+4(2-k2)[(1-2k)2+2]>0时,
设P1(x1,y1),P2(x2,y2),∴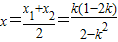 (1)
(1)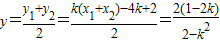 (2)
(2)
当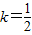 时,此时M(0,0).
时,此时M(0,0).
当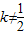 时,显然y≠0.此时(1)÷(2)得
时,显然y≠0.此时(1)÷(2)得 ,将其代入(2),
,将其代入(2),
得 .∵y≠0,∴有2x2-y2-4x+y=0.显然(0,0)也满足此方程.
.∵y≠0,∴有2x2-y2-4x+y=0.显然(0,0)也满足此方程.
当直线的斜率不存在时,此时直线方程为x=2,则P1P2中点为(2,0)符合上式.
综上可知,M点的轨迹方程为2x2-y2-4x+y=0.
点评:本题主要考查了直线与圆锥曲线的位置关系,考查了双曲线的性质,直线与曲线联立,根据方程的根与系数的关系解题是处理这类问题的最为常用的方法,但圆锥曲线的特点是计算量比较大,要求考生具备较强的运算推理,是难题.
(Ⅱ)由(Ⅰ)中的证明可知,|PF|为F(c,0)到l:bx-ay=0距离,由点到直线的距离公式列一个关于a,b,c的关系式,再由离心率得一关系式,结合a2+b2=c2求解a,b的值,则双曲线的方程可求;
(Ⅲ)分斜率存在和不存在得到过点A的直线方程,斜率存在时把直线方程和双曲线方程联立,利用根与系数关系得到M点的参数方程,消参后即可得到答案,然后验证斜率不存在时的情况.
解答:(Ⅰ)证明:右准线为
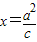 ,由对称性,不妨设渐近线l为
,由对称性,不妨设渐近线l为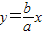 ,则
,则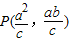 .
.又F(c,0),∴
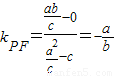 .
.又∵
 ,∴
,∴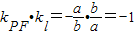 ,∴PF⊥l;
,∴PF⊥l;(Ⅱ)解:∵|PF|为F(c,0)到l:bx-ay=0距离,∴
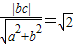 ,即b=
,即b=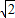 .
.又
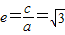 ,∴
,∴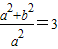 ,解得a2=1.
,解得a2=1.故双曲线方程为
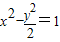 ;
;(Ⅲ)解:设M(x,y),
当过点A的直线斜率存在时,设直线方程为y-1=k(x-2),
由
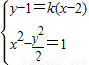 ,
,可得(2-k2)x2-2k(1-2k)x-(1-2k)2-2=0.
当(2-k2)≠0,△=(1-2k)24k2+4(2-k2)[(1-2k)2+2]>0时,
设P1(x1,y1),P2(x2,y2),∴
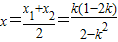 (1)
(1)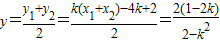 (2)
(2)当
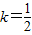 时,此时M(0,0).
时,此时M(0,0).当
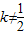 时,显然y≠0.此时(1)÷(2)得
时,显然y≠0.此时(1)÷(2)得 ,将其代入(2),
,将其代入(2),得
 .∵y≠0,∴有2x2-y2-4x+y=0.显然(0,0)也满足此方程.
.∵y≠0,∴有2x2-y2-4x+y=0.显然(0,0)也满足此方程.当直线的斜率不存在时,此时直线方程为x=2,则P1P2中点为(2,0)符合上式.
综上可知,M点的轨迹方程为2x2-y2-4x+y=0.
点评:本题主要考查了直线与圆锥曲线的位置关系,考查了双曲线的性质,直线与曲线联立,根据方程的根与系数的关系解题是处理这类问题的最为常用的方法,但圆锥曲线的特点是计算量比较大,要求考生具备较强的运算推理,是难题.

练习册系列答案
相关题目
 ,一条渐近线方程是
,一条渐近线方程是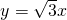 ,线段PQ是过曲线C右焦点F的一条弦,R是弦PQ的中点.
,线段PQ是过曲线C右焦点F的一条弦,R是弦PQ的中点.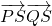 =0.当点P在曲线C上运动时,求a的取值范围.
=0.当点P在曲线C上运动时,求a的取值范围.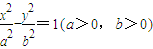 的右焦点为F,右准线为l,离心率为
的右焦点为F,右准线为l,离心率为 ,过y轴上一点A(0,b)作AM⊥l,垂足为M,则直线FM的斜率为 .
,过y轴上一点A(0,b)作AM⊥l,垂足为M,则直线FM的斜率为 .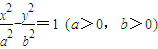 的右准线交x轴于A,虚轴的下端点为B,过双曲线的右焦点F(c,0)作垂直于x轴的直线交双曲线于P,过点A、B的直线与FP相交于点D,且
的右准线交x轴于A,虚轴的下端点为B,过双曲线的右焦点F(c,0)作垂直于x轴的直线交双曲线于P,过点A、B的直线与FP相交于点D,且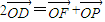 (O为坐标原点).
(O为坐标原点).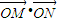 的取值范围.
的取值范围.