题目内容
(本题满分14分)数列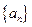 满足
满足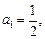
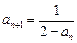 .
.
(1)求数列{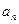 }的通项公式;(2)设数列{
}的通项公式;(2)设数列{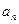 }的前
}的前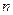 项和为
项和为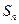 ,证明
,证明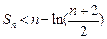 .
.
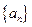 满足
满足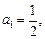
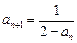 .
.(1)求数列{
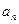 }的通项公式;(2)设数列{
}的通项公式;(2)设数列{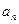 }的前
}的前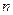 项和为
项和为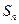 ,证明
,证明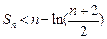 .
.(1)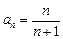
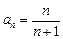
(1)方法一:∵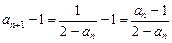 ,∴
,∴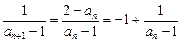 . --3分
. --3分
∴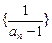 是首项为
是首项为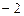 ,公差为
,公差为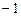 的等差数列.-4分∴
的等差数列.-4分∴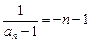 ,所以
,所以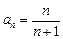 .6分
.6分
方法二: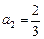 ,
,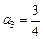 ,
,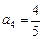 ,猜测
,猜测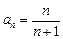 . -----2分
. -----2分
下用数学归纳法进行证明.
①当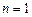 时,由题目已知可知
时,由题目已知可知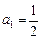 ,命题成立; --------------3分
,命题成立; --------------3分
②假设当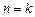 (
(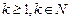 )时成立,即
)时成立,即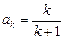 ,那么
,那么
当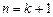 ,
,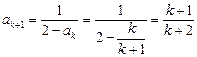 ,也就是说,当
,也就是说,当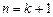 时命题也成立. ----5分
时命题也成立. ----5分
综上所述,数列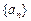 的通项公式为
的通项公式为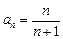 . ---6分
. ---6分
(2) 设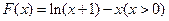 则
则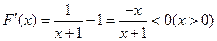 --------8分
--------8分
∴函数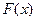 为
为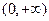 上的减函数,∴
上的减函数,∴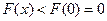 ,即
,即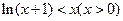
从而 -----10分
-----10分
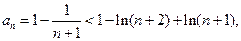 ----------11分
----------11分
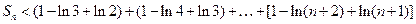 ---13分
---13分
∴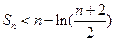 ----------14分
----------14分
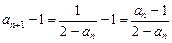 ,∴
,∴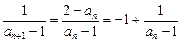 . --3分
. --3分∴
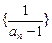 是首项为
是首项为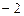 ,公差为
,公差为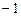 的等差数列.-4分∴
的等差数列.-4分∴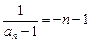 ,所以
,所以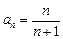 .6分
.6分方法二:
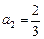 ,
,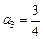 ,
,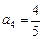 ,猜测
,猜测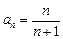 . -----2分
. -----2分下用数学归纳法进行证明.
①当
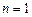 时,由题目已知可知
时,由题目已知可知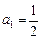 ,命题成立; --------------3分
,命题成立; --------------3分②假设当
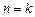 (
(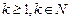 )时成立,即
)时成立,即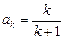 ,那么
,那么当
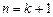 ,
,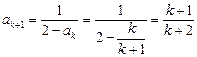 ,也就是说,当
,也就是说,当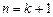 时命题也成立. ----5分
时命题也成立. ----5分综上所述,数列
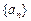 的通项公式为
的通项公式为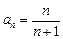 . ---6分
. ---6分(2) 设
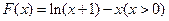 则
则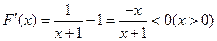 --------8分
--------8分∴函数
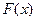 为
为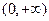 上的减函数,∴
上的减函数,∴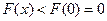 ,即
,即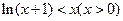
从而
 -----10分
-----10分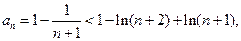 ----------11分
----------11分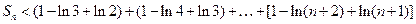 ---13分
---13分∴
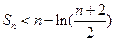 ----------14分
----------14分
练习册系列答案
相关题目
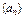 满足
满足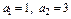 ,且
,且 。
。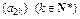 为等比数列;(2)求数列
为等比数列;(2)求数列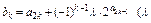 为非零常数)。试确定
为非零常数)。试确定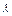 的值,使得对任意
的值,使得对任意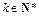 都有
都有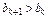 成立。
成立。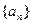 的首项为a1,公比q为正数(q≠1)的等比数列,其前n项和为Sn,且
的首项为a1,公比q为正数(q≠1)的等比数列,其前n项和为Sn,且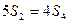 . (1)求q的值; (2)设
. (1)求q的值; (2)设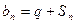 ,请判断数列
,请判断数列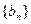 能否为等比数列,若能,请求出a1的值,否则请说明理由.
能否为等比数列,若能,请求出a1的值,否则请说明理由.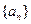 的前
的前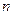 项和
项和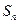 和通项
和通项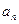 满足
满足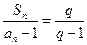 (
(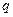 是常数且
是常数且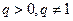 )。(Ⅰ)求数列
)。(Ⅰ)求数列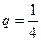 时,试证明
时,试证明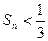 ;
;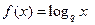 ,
,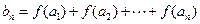 ,是否存在正整数
,是否存在正整数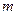 ,使
,使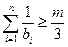 对
对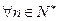 都成立?若存在,求出
都成立?若存在,求出 共有2m项,其中奇数项之和为90,偶数项之和为72,且
共有2m项,其中奇数项之和为90,偶数项之和为72,且 ,则该数列的公差为__________.
,则该数列的公差为__________.
 }的前n项和为
}的前n项和为 .若
.若 ,则
,则 =
= 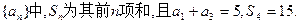 (I)求数列
(I)求数列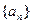 的通项公式; (II)设
的通项公式; (II)设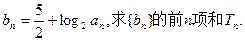
 满足
满足 ,
, ,且
,且 ,
, ,
, 成等差数列,则
成等差数列,则 的值是( )
的值是( )