题目内容
已知定圆Q:x2+y2-2x-15=0,动圆M和已知圆内切,且过点P(-1,0),
(1)求圆心M的轨迹及其方程;
(2)试确定m的范围,使得所求方程的曲线C上有两个不同的点关于直线l:y=4x+m对称.
(1)求圆心M的轨迹及其方程;
(2)试确定m的范围,使得所求方程的曲线C上有两个不同的点关于直线l:y=4x+m对称.
解 (1)已知圆可化为(x-1)2+y2=16,设动圆圆心M(x,y),则|MP|为半径,又圆M和圆Q内切,即|MP|+|MQ|=4,故M的轨迹是以P,Q为焦点的椭圆,且PQ中心为原点,故动圆圆心M的轨迹方程是
+
=1
(2)假设具有对称关系的两点所在直线l′的方程为y=-
x+n,代入椭圆方程中有3x2+4(-
x+n)2-12=0,即13x2-8nx+16n2-48=0.
若要椭圆上关于直线l对称得不同两点存在,则需l′与椭圆相交,且两交点P、Q到直线l的距离相等,即线段PQ的中点M在直线l上,
故△=64n2-4×13×(16n2-48)>0,∴-
<n<
.
设P(x1,y1),Q(x2,y2),
则x1+x2=
,y1+y2=-
(x1+x2)+2n=
n,∴
=4×
+m,
故m=-
,∴n=-
,
∴-
<-
<
,
即-
<m<
.
| x2 |
| 4 |
| y2 |
| 3 |
(2)假设具有对称关系的两点所在直线l′的方程为y=-
| 1 |
| 4 |
| 1 |
| 4 |
若要椭圆上关于直线l对称得不同两点存在,则需l′与椭圆相交,且两交点P、Q到直线l的距离相等,即线段PQ的中点M在直线l上,
故△=64n2-4×13×(16n2-48)>0,∴-
| ||
| 2 |
| ||
| 2 |
设P(x1,y1),Q(x2,y2),
则x1+x2=
| 8n |
| 13 |
| 1 |
| 4 |
| 24 |
| 13 |
| 12n |
| 13 |
| 4n |
| 13 |
故m=-
| 4n |
| 13 |
| 13m |
| 4 |
∴-
| ||
| 2 |
| 13m |
| 4 |
| ||
| 2 |
即-
2
| ||
| 13 |
2
| ||
| 13 |

练习册系列答案
相关题目
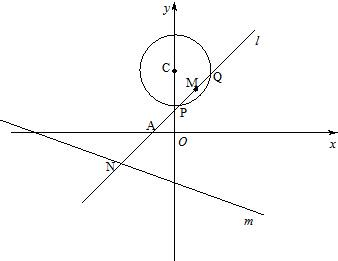 如图,已知定圆C:x2+(y-3)2=4,定直线m:x+3y+6=0,过A(-1,0)的一条动直线l与直线相交于N,与圆C相交于P,Q两点,M是PQ中点.
如图,已知定圆C:x2+(y-3)2=4,定直线m:x+3y+6=0,过A(-1,0)的一条动直线l与直线相交于N,与圆C相交于P,Q两点,M是PQ中点.