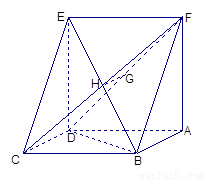
题目内容
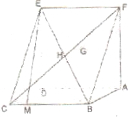 已知如图:平行四边形ABCD中,BC=2,CD=
已知如图:平行四边形ABCD中,BC=2,CD=| 2 |
(1)求证:GH∥平面CDE;
(2)求平面ECFE与平面ABCD所成的二面角的正弦值.
分析:(1)先根据ADEF是正方形得到G是AE的中点,再结合GH∥AB即可得到GH∥CD,进而得到结论;
(2)在平面DBC内过点D作DM⊥BC于M,连接EM,判断∠EMD是平面ECF与平面ABCD所成的二面角的平面角,求出其正弦值即可.
(2)在平面DBC内过点D作DM⊥BC于M,连接EM,判断∠EMD是平面ECF与平面ABCD所成的二面角的平面角,求出其正弦值即可.
解答: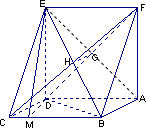 (1)证明:连接EA,
(1)证明:连接EA,
∵ADEF是正方形,∴G是AE的中点-------(1分)
∴在△EAB中,GH∥AB--(2分)
又∵AB∥CD,∴GH∥CD,--(3分)
∵HG?平面CDE,CD?平面CDE
∴GH∥平面CDE----(4分)
(2)解:在平面DBC内过点D作DM⊥BC于M,连接EM
∵BC⊥ED,∴BC⊥平面EMD
∵EM?平面EMD,∴BC⊥EM
∴∠EMD是平面ECF与平面ABCD所成的二面角的平面角-------(12分)
∵CD=
,BD=
∴DM=
BC=1,EM=
=
∴sin∠EMD=
=
即平面ECF与平面ABCD所成的二面角的正弦值为
 (1)证明:连接EA,
(1)证明:连接EA,∵ADEF是正方形,∴G是AE的中点-------(1分)
∴在△EAB中,GH∥AB--(2分)
又∵AB∥CD,∴GH∥CD,--(3分)
∵HG?平面CDE,CD?平面CDE
∴GH∥平面CDE----(4分)
(2)解:在平面DBC内过点D作DM⊥BC于M,连接EM
∵BC⊥ED,∴BC⊥平面EMD
∵EM?平面EMD,∴BC⊥EM
∴∠EMD是平面ECF与平面ABCD所成的二面角的平面角-------(12分)
∵CD=
| 2 |
| 2 |
∴DM=
| 1 |
| 2 |
| ED2+DM2 |
| 5 |
∴sin∠EMD=
| ED |
| EM |
2
| ||
| 5 |
即平面ECF与平面ABCD所成的二面角的正弦值为
2
| ||
| 5 |
点评:本题考查线面平行,考查面面角,解题的关键是掌握线面平行的判定,正确作出面面角.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
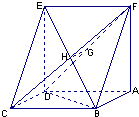 已知如图:平行四边形ABCD中,BC=2,BD⊥CD,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
已知如图:平行四边形ABCD中,BC=2,BD⊥CD,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.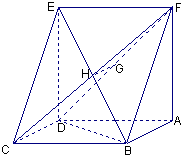 已知如图:平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
已知如图:平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点. 中,
中, ,
, ,
,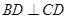 ,正方形
,正方形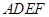 所在平面与平面
所在平面与平面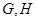 分别是
分别是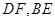 的中点。
的中点。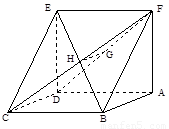
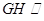 平面
平面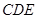 ;
;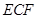 与平面
与平面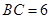 ,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.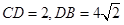 ,求四棱锥F-ABCD的体积.
,求四棱锥F-ABCD的体积.