题目内容
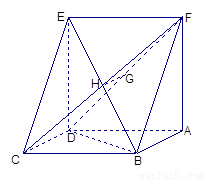
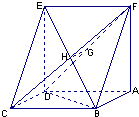 已知如图:平行四边形ABCD中,BC=2,BD⊥CD,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
已知如图:平行四边形ABCD中,BC=2,BD⊥CD,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.(1)求证:GH∥平面CDE;
(2)记CD=x,V(x)表示四棱锥F-ABCD体积,求V(x)的表达式;
(3)当V(x)取得最大值时,求平面ECF与平面ABCD所成的二面角的正弦值.
分析:(1)先根据ADEF是正方形得到G是AE的中点;再结合GH∥AB即可得到GH∥CD进而得到结论;
(2)先根据面面垂直的性质定理得到FA⊥平面ABCD;再求出四棱锥的底面积以及高,最后直接代入体积计算公式即可;
(3)先根据基本不等式求出V(x)取得最大值时对应的x;
解法1:在平面DBC内过点D作DM⊥BC于M,连接EM;通过分析得到∠EMD是平面ECF与平面ABCD所成的二面角的平面角;求出其正弦值即可;
解法2:以点D为坐标原定,DC所在的直线为x轴建立空间直角,求出个点对应坐标以及两个平面的法向量的坐标,再代入向量的夹角计算公式,得到余弦值,进而得到其正弦值.
(2)先根据面面垂直的性质定理得到FA⊥平面ABCD;再求出四棱锥的底面积以及高,最后直接代入体积计算公式即可;
(3)先根据基本不等式求出V(x)取得最大值时对应的x;
解法1:在平面DBC内过点D作DM⊥BC于M,连接EM;通过分析得到∠EMD是平面ECF与平面ABCD所成的二面角的平面角;求出其正弦值即可;
解法2:以点D为坐标原定,DC所在的直线为x轴建立空间直角,求出个点对应坐标以及两个平面的法向量的坐标,再代入向量的夹角计算公式,得到余弦值,进而得到其正弦值.
解答: (1):连接EA,∵ADEF是正方形
(1):连接EA,∵ADEF是正方形
∴G是AE的中点-------(1分)
∴在△EAB中,GH∥AB--(2分)
又∵AB∥CD,∴GH∥CD,--(3分)
∵HG?平面CDE,CD?平面CDE
∴GH∥平面CDE----(4分)
(2)∵平面ADEF⊥平面ABCD,交线为AD 且FA⊥AD,
∴FA⊥平面ABCD.-----(6分)
∵BD⊥CD,BC=2,CD=x
∴FA=2,BD=
(0<x<2)
∴S平行四边形ABCD=CD•BD=x
∴V(x)=
S平行四边形ABCD•FA=
x
(0<x<2)--(8分)
(3)要使V(x)取得最大值,只须x
=
(0<x<2)取得最大值,
∵x2(4-x2)≤(
)2=4,当且仅当x2=4-x2,即x=
时 V(x)取得最大值---(10分)
解法1:在平面DBC内过点D作DM⊥BC于M,连接EM
∵BC⊥ED
∴BC⊥平面EMD
∴BC⊥EM
∴∠EMD是平面ECF与平面ABCD所成的二面角的平面角-------(12分)
∵当V(x)取得最大值时,CD=
,DB=
∴DM=
BC=1,EM=
=
∴sin∠EMD=
=
 即平面ECF与平面ABCD所成的二面角的正弦值为
即平面ECF与平面ABCD所成的二面角的正弦值为
.-----------------(14分)
解法2:以点D为坐标原定,DC所在的直线为x轴建立空间直角
坐标系如图示,则D(0,0,0),C(
,0,0),B(0,
,0),E(0,0,2)
∴
=(0,0,
),
=(
,0,-2),
=(0,
,-2)-------(12分)
设平面ECF与平面ABCD所成的二面角为θ,
 平面ECF的法向量
平面ECF的法向量
=(a,b,c)
由
⊥
,
⊥
,得
a-2c=0,
b-2c=0
令c=1得
=(
,
,1)
又∵平面ABCD的法向量为
∴cosθ=
=
=
∴sinθ=
.-------(14分)
 (1):连接EA,∵ADEF是正方形
(1):连接EA,∵ADEF是正方形∴G是AE的中点-------(1分)
∴在△EAB中,GH∥AB--(2分)
又∵AB∥CD,∴GH∥CD,--(3分)
∵HG?平面CDE,CD?平面CDE
∴GH∥平面CDE----(4分)
(2)∵平面ADEF⊥平面ABCD,交线为AD 且FA⊥AD,
∴FA⊥平面ABCD.-----(6分)
∵BD⊥CD,BC=2,CD=x
∴FA=2,BD=
| 4-x2 |
∴S平行四边形ABCD=CD•BD=x
| 4-x2 |
∴V(x)=
| 1 |
| 3 |
| 2 |
| 3 |
| 4-x2 |
(3)要使V(x)取得最大值,只须x
| 4-x2 |
| x2(4-x2) |
∵x2(4-x2)≤(
| x2+4-x2 |
| 2 |
| 2 |
解法1:在平面DBC内过点D作DM⊥BC于M,连接EM
∵BC⊥ED
∴BC⊥平面EMD
∴BC⊥EM
∴∠EMD是平面ECF与平面ABCD所成的二面角的平面角-------(12分)
∵当V(x)取得最大值时,CD=
| 2 |
| 2 |
∴DM=
| 1 |
| 2 |
| ED2+DM2 |
| 5 |
∴sin∠EMD=
| ED |
| EM |
2
| ||
| 5 |
 即平面ECF与平面ABCD所成的二面角的正弦值为
即平面ECF与平面ABCD所成的二面角的正弦值为2
| ||
| 5 |
解法2:以点D为坐标原定,DC所在的直线为x轴建立空间直角
坐标系如图示,则D(0,0,0),C(
| 2 |
| 2 |
∴
| DE |
| 2 |
| EC |
| 2 |
| EB |
| 2 |
设平面ECF与平面ABCD所成的二面角为θ,
 平面ECF的法向量
平面ECF的法向量| n |
由
| n |
| EC |
| n |
| EB |
| 2 |
| 2 |
令c=1得
| n |
| 2 |
| 2 |
又∵平面ABCD的法向量为
| DE |
∴cosθ=
| ||||
|
| ||||
|
| ||
| 5 |
∴sinθ=
2
| ||
| 5 |
点评:本小题主要考查空间线面关系、二面角的度量、几何体的体积等知识.解决第二问得关键在于先根据面面垂直的性质定理得到FA⊥平面ABCD.

练习册系列答案
相关题目
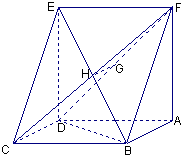 已知如图:平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
已知如图:平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.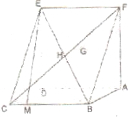 已知如图:平行四边形ABCD中,BC=2,
已知如图:平行四边形ABCD中,BC=2,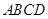 中,
中,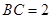 ,
,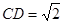 ,
,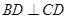 ,正方形
,正方形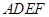 所在平面与平面
所在平面与平面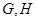 分别是
分别是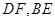 的中点。
的中点。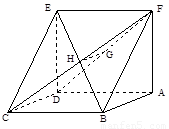
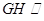 平面
平面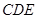 ;
;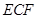 与平面
与平面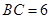 ,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.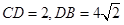 ,求四棱锥F-ABCD的体积.
,求四棱锥F-ABCD的体积.