题目内容
3．在△ABC中，已知$\overrightarrow{AB}$=（cos18°，cos72°），$\overrightarrow{BC}$=（2cos63°，2cos27°），则△ABC是（ ）| A． | 锐角三角形 | B． | 直角三角形 | C． | 钝角三角形 | D． | 无法确定 |
分析 利用数量积和三角公式得出$\overrightarrow{AB}$$•\overrightarrow{BC}$=2cos18°cos63°+2sin18°sin63°=2cos（18°-63°）=2sin45=$\sqrt{2}$＞0，判断向量$\overrightarrow{AB}$，$\overrightarrow{BC}$的夹角，即可得出∠B为钝角．
解答 解：∵$\overrightarrow{AB}$=（cos18°，cos72°），$\overrightarrow{BC}$=（2cos63°，2cos27°），
∴$\overrightarrow{AB}$=（cos18°，sin18°），$\overrightarrow{BC}$=（2cos63°，2sin63°），
∵$\overrightarrow{AB}$$•\overrightarrow{BC}$=2cos18°cos63°+2sin18°sin63°=2cos（18°-63°）=2sin45=$\sqrt{2}$＞0，
∴向量$\overrightarrow{AB}$，$\overrightarrow{BC}$的夹角为锐角，
∴∠B为钝角，
∴△ABC是钝角三角形．
点评 本题考查了平面向量与三角形的关系，数量积的运用判断三角形的形状，属于中档题，关键是判断三角形的夹角与向量的夹角的关系．
练习册系列答案
相关题目
14．为调查某社区居民的业余生活状况，研究这一社区居民在20：00-22：00时间段的休闲方式与性别的关系，随机调查了该社区80人，得到下面的数据表：
（Ⅰ）根据以上数据，能否有99%的把握认为“在20：00-22：00时间段居民的休闲方式与性别有关系”？
（Ⅱ）将此样本的频率估计为总体的概率，随机调查3名在该社区的男性，设调查的3人在这一时间段以看书为休闲方式的人数为随机变量X．求X的数学期望和方差．
附：X2=$\frac{n（{n}_{11}{n}_{22}-{n}_{12}{n}_{21}）^{2}}{{n}_{1}+{n}_{2}+n+{1}^{n}+2}$．
| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 | 10 | 50 | 60 |
| 女 | 10 | 10 | 20 |
| 合计 | 20 | 60 | 80 |
（Ⅱ）将此样本的频率估计为总体的概率，随机调查3名在该社区的男性，设调查的3人在这一时间段以看书为休闲方式的人数为随机变量X．求X的数学期望和方差．
| P（X2≥k） | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
12．
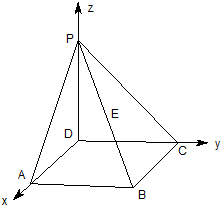PD垂直于正方形ABCD所在平面，AB=2，E为PB的中点，cos＜$\overrightarrow{DP}$，$\overrightarrow{AE}$＞=$\frac{\sqrt{3}}{3}$，若以如图所示建立空间直角坐标系，则E点坐标为（ ）
PD垂直于正方形ABCD所在平面，AB=2，E为PB的中点，cos＜$\overrightarrow{DP}$，$\overrightarrow{AE}$＞=$\frac{\sqrt{3}}{3}$，若以如图所示建立空间直角坐标系，则E点坐标为（ ）| A． | （1，1，2） | B． | （2，2，1） | C． | （1，1，1） | D． | $（1\;，\;1\;，\;\frac{1}{2}）$ |