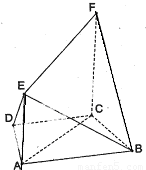
题目内容
如图所示,多面体FE-ABCD中,ABCD和ACFE都是直角梯形,DC∥AB,AE∥CF,平面ACFE⊥平面ABCD,AD=DC=CF=2AE=![]() ,∠ACF=∠ADC=
,∠ACF=∠ADC=![]() 。
。
(I)求证:BC⊥平面ACFE;
(II)求二面角B-FE-D的平面角的余弦值。
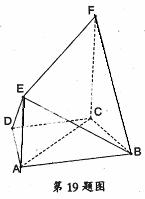
解:(Ⅰ)在直角梯形ABCD中,∵![]() ,又AD=DC=
,又AD=DC=![]() AB,可证BC⊥AC,
AB,可证BC⊥AC,
………2分
又∵平面ACFE⊥平面ABCD,且平面ACFE∩平面ABCD=AC,
∴BC⊥平面ACFE;………4分
(Ⅱ)以A为原点,分别以AB、AD、AE为x,y,z轴,建立空间直角坐标系,
设AE=a,则D(0, 2a,0),B(4a,0 ,0),E(0,0,a),F(2a,2a,2a), ………6分
设![]()
![]() 平面BEF,
平面BEF,![]() 平面DEF,
平面DEF,
![]() ,
,![]()
则
![]()
 ,
,![]()
………8分

![]()
 ,
,![]()
………9分

故所求二面角B-EF-D的平面角的余弦值是![]() . ………12分
. ………12分

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
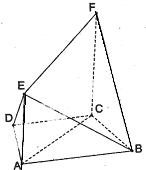 (2012•安庆二模)如图所示,多面体FE-ABCD中,ABCD和ACFE都是直角梯形,DC∥AB,AE∥CF,平面ACFE⊥平面ABCD,AD=DC=CF=2AE=
(2012•安庆二模)如图所示,多面体FE-ABCD中,ABCD和ACFE都是直角梯形,DC∥AB,AE∥CF,平面ACFE⊥平面ABCD,AD=DC=CF=2AE=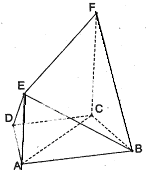 如图所示,多面体FE-ABCD中,ABCD和ACFE都是直角梯形,DC∥AB,AE∥CF,平面ACFE⊥平面ABCD,AD=DC=CF=2AE=
如图所示,多面体FE-ABCD中,ABCD和ACFE都是直角梯形,DC∥AB,AE∥CF,平面ACFE⊥平面ABCD,AD=DC=CF=2AE= ,∠ACF=∠ADC=
,∠ACF=∠ADC= .
.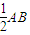 ,∠ACF=∠ADC=
,∠ACF=∠ADC=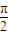 .
.