Question

如图，在棱长为1的正方体AC₁中，E、F分别为A₁D₁和A₁B₁的中点．
（1）求异面直线AE和BF所成的角的余弦值；
（2）求平面BDD₁与平面BFC₁所成的锐二面角的余弦值；
（3）若点P在正方形ABCD内部或其边界上，且EP∥平面BFC₁，求EP的最大值、最小值．

Answer 1

分析：因为是正方体，很容易建系，研究的问题主要是空间角，易用向量法求解，所以先建立空间直角坐标系．（1）分别求得A，E，B，F点的坐标，再求得相应向量的坐标，最后由向量的夹角公式求解．（2）设平面BDD₁与平面BFC₁的一个法向量，用数量积为零求得，然后，用这两个法向量，利用向量的夹角公式求解．（3）设点P的坐标为：P（x，y，0）（0≤x≤1，0≤y≤1），则由

EP

•

n

=0得(x-

1

2

)+2y-1=0，从而建立∴|

EP

|=

(x- 1 2 )2+y2+1

=

(2y-1)2+y2+1

=

5y2-4y+2

=

5(y- 2 5 )2+ 6 5

二次函数模型求解最值．

解答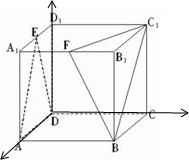：解：以D为原点建立如图所示空间直角坐标系
（1）A（1，0，0），E(

1

2

，0，1)，
B（1，1，0），F(1，

1

2

，1)，

AE

=(-

1

2

，0，1)，

BF

=(0，-

1

2

，1)，cos(

AE

，

BF

)=

1

5 4 5 4

=

4

5

；
故异面直线AE和BF所成的角的余弦值为

4

5

．
（2）平面BDD₁的一个法向量为

MA

=(

1

2

，-

1

2

，0)
设平面BFC₁的法向量为

n

=(x，y，z)

n • BF =- 1 2 y+z=0 n • BC =(x，y，z)•(-1，0，1)=-x+z=0

∴

x=z y=2z

取z=1得平面BFC₁的一个法向量

n

=(1，2，1)
cos＜

MA

，

n

＞=

MA • n

| MA || n |

=

1 2 -1

2 2 6

=-

3

6

∴所求的余弦值为

3

6

；
（3）设

EP

=(x-

1

2

，y，-1)，由

EP

•

n

=0得(x-

1

2

)+2y-1=0
即x=-2y+

3

2

，0≤x≤1，∴0≤-2y+

3

2

≤1，解得

1

4

≤y≤

3

4

∴|

EP

|=

(x- 1 2 )2+y2+1

=

(2y-1)2+y2+1

=

5y2-4y+2

=

5(y- 2 5 )2+ 6 5

∵

1

4

≤y≤

3

4

∴当y=

2

5

时，∴|

EP

|min=

30

5

当y=

3

4

时，∴|

EP

|max=

29

4

．

点评：本题主要考查异面直线所成的角，二面角及两点间的距离问题，同时，还考查了向量法和转化思想，是常考类型，属中档题．