题目内容
(2012•芜湖二模)设函数f(x)=
(a>0)
(1)若函数f(x)在x=-1处取得极值-2,求a,b的值.
(2)若函数f(x)在区间(-1,1)内单调递增,求b的取值范围.
| ax | x2+b |
(1)若函数f(x)在x=-1处取得极值-2,求a,b的值.
(2)若函数f(x)在区间(-1,1)内单调递增,求b的取值范围.
分析:(1)对f(x)进行求导,根据已知条件函数f(x)在x=-1处取得极值-2,可得f′(-1)=0,和f(-1)=2,分别解出a,b的值;
(2)需要对b进行讨论:b≤0和b>0两种情况,利用导数研究函数的单调性,根据f′(x)>0在区间(-1,1)内大于0,求出b的范围;
(2)需要对b进行讨论:b≤0和b>0两种情况,利用导数研究函数的单调性,根据f′(x)>0在区间(-1,1)内大于0,求出b的范围;
解答:(1)∵函数f(x)=
(a>0)
函数f(x)在x=-1处取得极值-2,
f′(x)=
依题意:
⇒
…(6分)
(2)f′(x)=
,
∵a>0,
∴当b≤0时f'(x)≤0,函数f(x)在(-1,1)内不可能增,舍去;
当b>0,时
f′(x)=
若x∈(-
,
)时
f'(x)>0,
f(x)递增,
∴(-1,1)⊆(-
,
)
∴
⇒b≥1,
故所求范围为[1,+∞)…(12分)
| ax |
| x2+b |
函数f(x)在x=-1处取得极值-2,
f′(x)=
| a(b-x2) |
| (x2+b)2 |
依题意:
|
|
(2)f′(x)=
| -a(x2-b) |
| (x2+b)2 |
∵a>0,
∴当b≤0时f'(x)≤0,函数f(x)在(-1,1)内不可能增,舍去;
当b>0,时
f′(x)=
-a(x+
| ||||
| (x2+b)2 |
| b |
| b |
f'(x)>0,
f(x)递增,
∴(-1,1)⊆(-
| b |
| b |
∴
|
故所求范围为[1,+∞)…(12分)
点评:此题主要考查利用导数研究函数的极值问题,是一道基础题,比较简单,解题过程中用到了分类讨论的思想;

练习册系列答案
相关题目
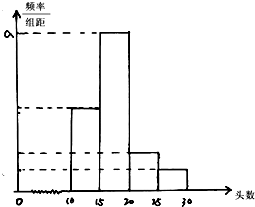 (2012•芜湖二模)某省对省内养殖场“瘦肉精”使用情况进行检查,在全省的养殖场随机抽取M个养殖场的猪作为样本,得到M个养殖场“瘦肉精”检测阳性猪的头数,根据此数据作出了频率分布表和频率分布直方图如下:
(2012•芜湖二模)某省对省内养殖场“瘦肉精”使用情况进行检查,在全省的养殖场随机抽取M个养殖场的猪作为样本,得到M个养殖场“瘦肉精”检测阳性猪的头数,根据此数据作出了频率分布表和频率分布直方图如下: