题目内容
等差数列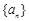 的公差
的公差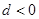 ,且
,且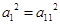 ,则数列
,则数列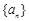 的前n项和
的前n项和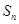 取最大值时
取最大值时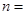 ( )
( )
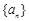 的公差
的公差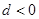 ,且
,且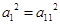 ,则数列
,则数列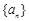 的前n项和
的前n项和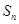 取最大值时
取最大值时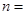 ( )
( )| A.6 | B.5 | C.5或6 | D.6或7 |
C
分析:由题意可得:
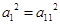 ,即(a
,即(a +a
+a )(a
)(a -a
-a )=0,结合题意可得:a
)=0,结合题意可得:a +a
+a =0结合等差数列的性质可得:2a
=0结合等差数列的性质可得:2a =0,又公差d<0,所以此数列从第7项开始,以后每项都小于0,所以Sn取得最大值时的项数n=5或者n=6.
=0,又公差d<0,所以此数列从第7项开始,以后每项都小于0,所以Sn取得最大值时的项数n=5或者n=6.解答:解:由题意可得:a
 =a
=a ,即(a
,即(a +a
+a )(a
)(a -a
-a )=0,
)=0,因为等差数列{an}的公差d<0,
所以a
 +a
+a =0
=0所以2a
 =0,所以此数列从第7项开始,以后每项都小于0,
=0,所以此数列从第7项开始,以后每项都小于0,所以S
 取得最大值时的项数n=5或者n=6.
取得最大值时的项数n=5或者n=6.故答案为:5或6.选C。

练习册系列答案
相关题目
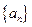 满足
满足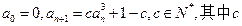 为实数
为实数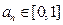 对任意
对任意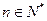 成立的充分必要条件是
成立的充分必要条件是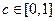 ;
;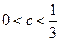 ,证明:
,证明: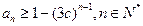 ;
;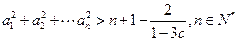
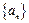 的各项均是正数,其前
的各项均是正数,其前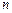 项和为
项和为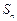 ,满足
,满足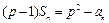 ,其中
,其中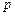 为正常数,且
为正常数,且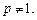
 (1)求数列
(1)求数列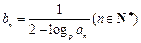 ,数列
,数列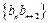 的前
的前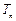 ,求证:
,求证: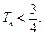
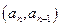 在直线
在直线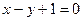 上,
上, 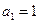 ,
,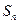 是数列
是数列 的前n项和,数列
的前n项和,数列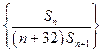 的最大值为
的最大值为  的前n项和为
的前n项和为 ,且4
,且4 ,2
,2 ,
, 成等差数列。若
成等差数列。若 ="( " )
="( " )