题目内容
【题目】国内,某知名连接店分店开张营业期间,在固定的时间段内消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖的有效展开,参与抽奖活动的人数越来越多,该分店经理对开业前7天参加抽奖活动的人数进行统计, ![]() 表示开业第
表示开业第![]() 天参加抽奖活动的人数,得到统计表格如下:
天参加抽奖活动的人数,得到统计表格如下:

经过进一步的统计分析,发现![]() 与
与![]() 具有线性相关关系.
具有线性相关关系.
(1)如从这7天中随便机抽取两天,求至少有1天参加抽奖人数超过10天的概率;
(2)根据上表给出的数据,用最小二乘法,求出![]() 与
与![]() 的线性回归方程
的线性回归方程![]() ,并估计若该活动持续10天,共有多少名顾客参加抽奖.
,并估计若该活动持续10天,共有多少名顾客参加抽奖.
参考公式: 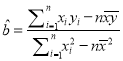 ,
, ![]() ,
, ![]() ,
, ![]() .
.
【答案】(1)![]() (2)140
(2)140
【解析】试题分析:(1)先利用枚举法确定7天中随便机抽取两天总事件数,从中确定至少有1天参加抽奖人数超过10的事件数,最后根据古典概型概率公式求概率,(2)先求平均数![]() ,代入公式
,代入公式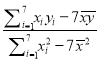 求
求![]() ,利用
,利用![]() 求
求![]() ,即得线性回归方程,再利用线性回归方程估计
,即得线性回归方程,再利用线性回归方程估计![]() 时参加抽奖的人数,得到此次抽奖活动总人数.
时参加抽奖的人数,得到此次抽奖活动总人数.
试题解析:(Ⅰ)这7天中参加抽奖的人数没有超过10的为第1,2,3,4天,超过10的为第5,6,7天,从这7天中任取两天的情况有![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,共21种,其中至少有1天参加抽奖人数超过10的有15种,所以
,共21种,其中至少有1天参加抽奖人数超过10的有15种,所以![]() .
.
(Ⅱ)依题意: ![]() .
.
![]() ,
, ![]() ,
, ![]() ,
,
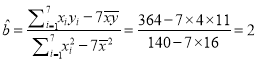 ,
, ![]() ,
,
则![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,
,
预测![]() 时
时![]() ,
, ![]() 时,
时, ![]() ,
, ![]() 时
时![]() ,
,
则此次活动参加抽奖的人数约为![]() 人.
人.

练习册系列答案
相关题目