题目内容
已知二次函数 .
.
(1)若对任意 、
、 ,且
,且 ,都有
,都有 ,求证:关于
,求证:关于 的方程
的方程
 有两个不相等的实数根且必有一个根属于
有两个不相等的实数根且必有一个根属于 ;
;
(2)若关于 的方程
的方程 在
在 上的根为
上的根为 ,且
,且 ,设函数
,设函数 的图象的对称轴方程为
的图象的对称轴方程为 ,求证:
,求证: .
.
【答案】
(1)详见解析;(2)详见解析.
【解析】
试题分析:(1)先构造新函数 ,利用
,利用 证明方程
证明方程
 有两个不相等的实数根,然后利用存在定理证明方程
有两个不相等的实数根,然后利用存在定理证明方程 必有一个根属于
必有一个根属于 ,即利用
,即利用 来证明;(2)将
来证明;(2)将 的代入方程
的代入方程 得到
得到 的表达式,结合
的表达式,结合 证明
证明 .
.
试题解析:(1)构造函数

 ,
,
由于函数 为二次函数,所以
为二次函数,所以 ,
,
对于二次函数 而言,
而言,


 ,
,
若 ,则有
,则有 且有
且有 ,从而有
,从而有 ,这与
,这与 矛盾,
矛盾,
故 ,故方程
,故方程 有两个不相等,
有两个不相等,
由于 ,
,
 ,
,
所以 ,
,
由零点存在定理知,方程 必有一个根属于
必有一个根属于 ;
;
(2)由题意知 ,化简得
,化简得 ,
,
即 ,则有
,则有 ,
, ,
,
由于 ,则
,则 ,故
,故 ,即
,即 .
.
考点:1.二次方程根的个数的判断;2.零点存在定理;3.二次函数图象的对称轴

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 在x=1处的导数值为1,则该函数的最大值是 (
)
在x=1处的导数值为1,则该函数的最大值是 (
)
 B.
B. C.
C. D.
D.
 。
。 的图像经过怎样平移得来;
的图像经过怎样平移得来;
 .
. ,试判断函数
,试判断函数 零点个数;
零点个数; 且
且 ,
, ,试证明
,试证明 ,使
,使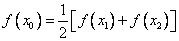 成立。
成立。 ,使
,使 同时满足以下条件①对
同时满足以下条件①对 ,且
,且 ;②对
;②对 ,都有
,都有 。若存在,求出
。若存在,求出 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。