题目内容
已知二次函数![]() ,
,
(1)当![]() 时,
时,![]() 在 [ – 1,1 ] 上的最大值为
在 [ – 1,1 ] 上的最大值为![]() ,求
,求![]() 的最小值;
的最小值;
(2)对于任意的![]() ,总有
,总有![]() ,求a的取值范围;
,求a的取值范围;
(3)若当![]() 时,记
时,记![]() ,令a = 1,求证:
,令a = 1,求证:![]() 成立.
成立.
(1)![]() (2)
(2)![]() 且
且![]() (3)见解析
(3)见解析
解析:
(1) 由![]() 知
知![]() ,当x = 1时,解得最大值为
,当x = 1时,解得最大值为![]() ,即
,即![]()
∴ ![]() ∴
∴ ![]()
(2) 由题意知:当 t = 0时,![]() 使
使![]() 成立
成立
当![]() 时,有
时,有
对任意的![]() 恒成立
恒成立
∵ ![]()
∴ ![]() 或
或![]() ,则
,则![]()
![]() 要使①②成立,则
要使①②成立,则![]()
而![]() ,综上所述,
,综上所述,![]() 且
且![]()
(3) 由题意:![]()
令![]()
∴ ![]()
∴ ![]()
∴ ![]() 在
在![]() 个
个
∴ ![]()
又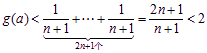
∴ 原结论成立

练习册系列答案
相关题目
 在x=1处的导数值为1,则该函数的最大值是 (
)
在x=1处的导数值为1,则该函数的最大值是 (
)
 B.
B. C.
C. D.
D.
 。
。 的图像经过怎样平移得来;
的图像经过怎样平移得来;
 .
. ,试判断函数
,试判断函数 零点个数;
零点个数; 且
且 ,
, ,试证明
,试证明 ,使
,使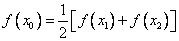 成立。
成立。 ,使
,使 同时满足以下条件①对
同时满足以下条件①对 ,且
,且 ;②对
;②对 ,都有
,都有 。若存在,求出
。若存在,求出 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。