题目内容
已知△ABC中,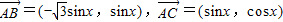
(1)设
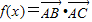 ,若f(A)=0,求角A的值;
,若f(A)=0,求角A的值;(2)若对任意的实数t,恒有
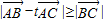 ,求△ABC面积的最大值.
,求△ABC面积的最大值.
【答案】分析:(1)利用数量积公式求得f(x)=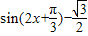 ,再由 f(A)=0求得
,再由 f(A)=0求得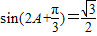 ,故有
,故有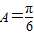 .
.
(2)由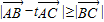 可得BC⊥AC,再由
可得BC⊥AC,再由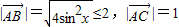 ,求得BC≤
,求得BC≤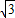 ,由此根据△ABC面积
,由此根据△ABC面积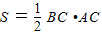 求得它的最大值.
求得它的最大值.
解答:解:(1)∵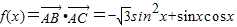 =
=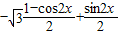 =
=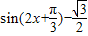
∵f(A)=0=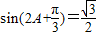 ,且
,且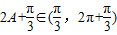 ,∴
,∴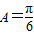 .(7分)
.(7分)
(2)∵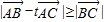 ,故点B到直线AC的最短距离为BC,∴BC⊥AC.
,故点B到直线AC的最短距离为BC,∴BC⊥AC.
∵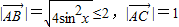 ,∴由勾股定理可得 BC=
,∴由勾股定理可得 BC=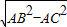 ≤
≤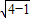 =
=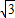 ,
,
故△ABC面积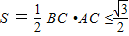 ,
,
故△ABC面积的最大值为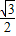 .(14分)
.(14分)
点评:本题主要考查两个向量的数量积的定义,数量积公式的应用,两个向量垂直的性质,属于中档题.
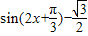 ,再由 f(A)=0求得
,再由 f(A)=0求得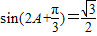 ,故有
,故有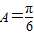 .
.(2)由
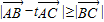 可得BC⊥AC,再由
可得BC⊥AC,再由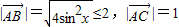 ,求得BC≤
,求得BC≤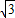 ,由此根据△ABC面积
,由此根据△ABC面积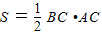 求得它的最大值.
求得它的最大值.解答:解:(1)∵
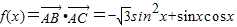 =
=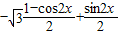 =
=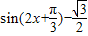
∵f(A)=0=
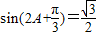 ,且
,且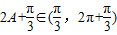 ,∴
,∴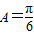 .(7分)
.(7分)(2)∵
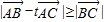 ,故点B到直线AC的最短距离为BC,∴BC⊥AC.
,故点B到直线AC的最短距离为BC,∴BC⊥AC.∵
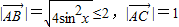 ,∴由勾股定理可得 BC=
,∴由勾股定理可得 BC=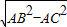 ≤
≤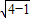 =
=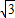 ,
,故△ABC面积
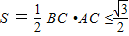 ,
,故△ABC面积的最大值为
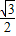 .(14分)
.(14分)点评:本题主要考查两个向量的数量积的定义,数量积公式的应用,两个向量垂直的性质,属于中档题.

练习册系列答案
相关题目