题目内容
(2011•泉州模拟)已知△ABC中,AC=1,∠ABC=
,D为BC中点,则△ABD的最大面积是
.
| π |
| 3 |
| ||
| 8 |
| ||
| 8 |
分析:利用余弦定理通过基本不等式求出ac的最大值,然后利用D为BC中点,则△ABD的最大面积.
解答:解:因为D为BC中点,则△ABD的面积是三角形ABC面积的一半,
由余弦定理可知1=a2+c2-2accos60°,
即1=a2+c2-ac≥2ac-ac=ac,所以ac≤1,当且仅当a=c时等号成立.
S△ABD=
S△ABC=
×
acsinB≤
.
故答案为:
.
由余弦定理可知1=a2+c2-2accos60°,
即1=a2+c2-ac≥2ac-ac=ac,所以ac≤1,当且仅当a=c时等号成立.
S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 8 |
故答案为:
| ||
| 8 |
点评:本题是中档题,考查余弦定理的应用,三角形的面积求法,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

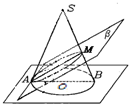 (2011•泉州模拟)如图所示,圆锥SO的轴截面△SAB是边长为4的正三角形,M为母线SB的中点,过直线AM作平面β⊥面SAB,设β与圆锥侧面的交线为椭圆C,则椭圆C的短半轴为( )
(2011•泉州模拟)如图所示,圆锥SO的轴截面△SAB是边长为4的正三角形,M为母线SB的中点,过直线AM作平面β⊥面SAB,设β与圆锥侧面的交线为椭圆C,则椭圆C的短半轴为( )