题目内容
(本题满分13分)某商场举行抽奖活动,从装有编号0,1,2,3四个球的抽奖箱中,每次取出后放回,连续取两次,取出的两个小球号码相加之和等于5中一等奖,等于4中二等奖,等于3中三等奖。
(1)求中二等奖的概率;
(2)求未中奖的概率。
【答案】
(1) ;(2)
;(2)
【解析】
试题分析:(1)设“中二等奖”的事件为A,
所有基本事件包括 共16个,
共16个,
事件A包含基本事件 共3个,
共3个,
所以 ……6分
……6分
(2)设“未中奖”的事件为B ,
所有基本事件包括 共16个,
共16个,
“两个小球号码相加之和等于3”这一事件包括基本事件 共4个,
共4个,
“两个小球号码相加之和等于5”这一事件包括基本事件 共2个
共2个
 ……12分答:中二等奖概率为
……12分答:中二等奖概率为 ,未中奖的概率为
,未中奖的概率为 ……13分
……13分
考点:本小题主要考查古典概型概率的求法,考查学生的列举、归纳的能力.
点评:求古典概型的概率时,一定要把基本事件一一列举出来,要做到不重不漏,另外还要注意解答题的步骤要规范.

练习册系列答案
相关题目
(本题满分1 3分)
3分)
某运动员进行20次射击练习,记录了他射击的有关数据,得到下表:
| 环数 | 7 | 8 | 9 | 10 |
| 命中次数 | 2 | 7 | 8 | 3 |
(Ⅰ)求此运动员射击的环数的平均数;
(Ⅱ)若将表中某一环数所对应的命中次数作为一个结果,在四个结果(2次、7次、8次、3次)中,随机取2个不同的结果作为基本事件进行研究,记这两个结果分别为
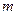 次、
次、 次,每个基本事件为(m,n).
次,每个基本事件为(m,n).求“
 ”的概率.
”的概率.  与
与 大小, 并写出完成总任务的时间
大小, 并写出完成总任务的时间 的表达式;
的表达式; (百台),其总成本为
(百台),其总成本为 (万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为2万元(总成本=固定成本+生产成本).销售收入
(万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为2万元(总成本=固定成本+生产成本).销售收入 (万元)满足
(万元)满足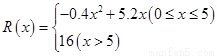 ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题: 的解析式(利润=销售收入—总成本);
的解析式(利润=销售收入—总成本); 元(
元( ,设该食品厂每公斤蘑菇的出厂价为
,设该食品厂每公斤蘑菇的出厂价为 元(
元( ),根据市场调查,销售量
),根据市场调查,销售量 与
与 成反比,当每公斤蘑菇的出厂价为30元时,日销售量为100公斤.
成反比,当每公斤蘑菇的出厂价为30元时,日销售量为100公斤. 元与每公斤蘑菇的出厂价
元与每公斤蘑菇的出厂价 ,当每公斤蘑菇的出厂价
,当每公斤蘑菇的出厂价 元(
元( ,设该食品厂每公斤蘑菇的出厂价为
,设该食品厂每公斤蘑菇的出厂价为 元(
元( ),根据市场调查,销售量
),根据市场调查,销售量 与
与 成反比,当每公斤蘑菇的出厂价为30元时,日销售量为100公斤.
成反比,当每公斤蘑菇的出厂价为30元时,日销售量为100公斤. 元与每公斤蘑菇的出厂价
元与每公斤蘑菇的出厂价 ,当每公斤蘑菇的出厂价
,当每公斤蘑菇的出厂价