题目内容
记函数 的定义域为A,
的定义域为A, 的定义域为B,
的定义域为B,
(Ⅰ)若 ,求A∩B;
,求A∩B;
(Ⅱ)若B⊆A,求实数a的取值范围.
解:(1)要使f(x)有意义,则 ,解得-1<x<1,
,解得-1<x<1,
所以A={x|-1<x<1},
要使g(x)有意义,则 ,因为a<1,解得:2a<x≤a+1,
,因为a<1,解得:2a<x≤a+1,
所以B={x|2a<x≤a+1},
当a= 时,B={x|
时,B={x|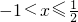 },
},
所以A∩B={x|-1<x≤ };
};
(2)由B⊆A得: 解得:
解得: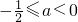 ,
,
所以使B⊆A的实数a的取值范围[ ,0).
,0).
分析:(1)根据两函数的解析式有意义求出集合A和集合B,把a=- 代入后化简集合B,然后直接取交集;
代入后化简集合B,然后直接取交集;
(2)由集合B是集合A的子集,且集合B非空,根据端点值列不等式求解实数a的取值范围.
点评:本题主要考查集合的交集和子集概念,属于基础题.要正确处理两集合的包含关系,必须对子集的概念有深刻的理解,善于抓住端点值的关系,正确列出相应等式.
 ,解得-1<x<1,
,解得-1<x<1,所以A={x|-1<x<1},
要使g(x)有意义,则
 ,因为a<1,解得:2a<x≤a+1,
,因为a<1,解得:2a<x≤a+1,所以B={x|2a<x≤a+1},
当a=
 时,B={x|
时,B={x|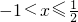 },
},所以A∩B={x|-1<x≤
 };
};(2)由B⊆A得:
 解得:
解得: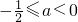 ,
,所以使B⊆A的实数a的取值范围[
 ,0).
,0).分析:(1)根据两函数的解析式有意义求出集合A和集合B,把a=-
 代入后化简集合B,然后直接取交集;
代入后化简集合B,然后直接取交集;(2)由集合B是集合A的子集,且集合B非空,根据端点值列不等式求解实数a的取值范围.
点评:本题主要考查集合的交集和子集概念,属于基础题.要正确处理两集合的包含关系,必须对子集的概念有深刻的理解,善于抓住端点值的关系,正确列出相应等式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的定义域为A,函数
的定义域为A,函数 的定义域为B.
的定义域为B. 的定义域为A,
的定义域为A,
 的定义域为B.
的定义域为B. ,求实数
,求实数 的取值范围.
的取值范围. 的定义域为A,则
的定义域为A,则 中有 个元素。
中有 个元素。 的定义域为A,
的定义域为A, (a < 1)的定义域为B.
(a < 1)的定义域为B. ,求实数a的取值范围.
,求实数a的取值范围.