题目内容
(本小题满分14分)如图,将一副三角板拼接,使他们有公共边BC,且使这两个三角形所在的平面互相垂直, ,
, ,
, ,BC=6.
,BC=6.

(1)证明:平面ADC平面ADB;
(2)求B到平面ADC的距离.
(1)证明见解析;(2)
【解析】
试题分析:(1)解决立体几何的有关问题,空间想象能力是非常重要的,但新旧知识的迁移融合也很重要,在平面几何的基础上,把某些空间问题转化为平面问题来解决,有时很方便;(2)证明两个平面垂直,首先考虑直线与平面垂直,也可以简单记为“证面面垂直,找线面垂直”,是化归思想的体现,这种思想方法与空间中的平行关系的证明类似,掌握化归与转化思想方法是解决这类题的关键;(3)证明线面垂直的方法:一是线面垂直的判定定理;二是利用面面垂直的性质定理;三是平行线法(若两条平行线中的一条垂直于这个平面,则另一条也垂直于这个平面.解题时,注意线线、线面与面面关系的相互转化.
试题解析:(1)证明:因为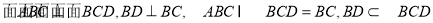 ,
,
所以 . (3分)
. (3分)
又 ,所以
,所以 . (4分)
. (4分)
又 ,且
,且 ,
,
所以 . (5分)
. (5分)
又 ,所以
,所以 .(6分)
.(6分)
(2)在 中,
中, ,得
,得 ,(7分)
,(7分)
在等腰 中,
中, ,得
,得 . (8分)
. (8分)
由(1)知 ,所以
,所以 , (9分)
, (9分)
在 中,
中, ,
, ,得
,得 ,(10分)
,(10分)
又 ,设
,设 到面
到面 的距离为
的距离为 ,
,
由 , (12分)
, (12分)
得 , (13分)
, (13分)
解得 ,即B到平面ADC的距离
,即B到平面ADC的距离 . (14分)
. (14分)
考点:1、平面与平面垂直的判定;2、点到平面的距离.

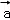 ,
, 满足|
满足| +
+ |=
|=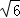 ,|
,| B.
B.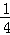 C.
C.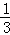 D.
D.
 则
则 的值为( )
的值为( )  B.
B. C.
C. D.
D.
 ,则
,则 = .
= . ,
, ”的否定是
”的否定是 ,
, B.
B. ,
, ,
, D.
D.
 ,
, ,则
,则 的最小值是 .
的最小值是 .  B.
B.
 D.
D.
 的解集为
的解集为 ,则实数
,则实数 .
. 的展开式中,记
的展开式中,记 项的系数为f(
项的系数为f( ,
, ),则f(3,0)+f(2,1)+f(1,2)+f(0,3) = .
),则f(3,0)+f(2,1)+f(1,2)+f(0,3) = .