题目内容
已知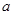 为实数,
为实数,
(1)若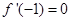 ,求
,求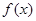 在
在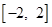 上最大值和最小值;
上最大值和最小值;
(2)若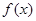 在
在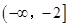 和
和 上都是递增的,求
上都是递增的,求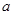 的取值范围。
的取值范围。
【答案】
(1) ;(2)
;(2) 。
。
【解析】
试题分析:(1) ,由
,由 得
得 3分
3分
此时 4分
4分
令 得
得 5分
5分
当 变化时,
变化时, 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
0 |
↗ |
极大值 |
↘ |
极小值 |
↗ |
0 |
 8分
8分
(2) 的图象为开口向上且过点
的图象为开口向上且过点 的抛物线。 9分
的抛物线。 9分
 在
在 和
和 上都是递增的,
上都是递增的,
 当
当 或
或 时,
时, 恒成立,
11分
恒成立,
11分
则
故 的取值范围为
的取值范围为 14分
14分
考点:利用导数研究函数的最值;利用导数研究函数的单调性。
点评:我们可以利用导数研究函数的单调性、极值和最值。再利用导数研究函数的单调性时,我们一定要注意:若函数 在区间D内是单调递增的,我们应得到:
在区间D内是单调递增的,我们应得到: 在区间D内恒成立,且不恒为0。此为易错点,一定要引起我们的重视。
在区间D内恒成立,且不恒为0。此为易错点,一定要引起我们的重视。

练习册系列答案
相关题目











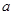 为实数,
为实数,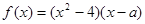
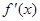 ;
; ,求
,求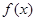 在[-2,2] 上的最大值和最小值;
在[-2,2] 上的最大值和最小值;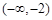 和
和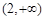 上都是递增的,求
上都是递增的,求 为实数.
为实数. ,求
,求 ;
; ,求
,求 ,
, 的值.
的值. 为实数,
为实数, (1)求导数
(1)求导数 ;(2)若
;(2)若 ,求
,求 在
在 上的最大值和最小值
上的最大值和最小值