题目内容
已知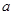 为实数,
为实数,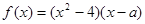
(1)求导数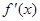 ;
;
(2)若 ,求
,求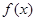 在[-2,2] 上的最大值和最小值;
在[-2,2] 上的最大值和最小值;
(3)若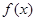 在
在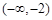 和
和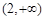 上都是递增的,求
上都是递增的,求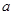 的取值范围.
的取值范围.
【答案】
(1)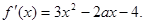 (2)最大值为
(2)最大值为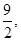 最小值为
最小值为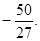 (3)
(3)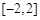
【解析】
试题分析:⑴由原式得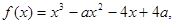 ∴
∴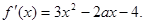 ………3分
………3分
⑵由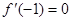 得
得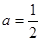 ,此时有
,此时有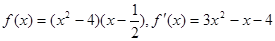 .
.
由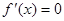 得
得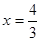 或x="-1" , 又
或x="-1" , 又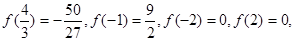
所以f(x)在[-2,2]上的最大值为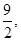 最小值为
最小值为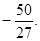 …………………8分
…………………8分
⑶解法一: 的图象为开口向上且过点(0,-4)的抛物线,由条件得
的图象为开口向上且过点(0,-4)的抛物线,由条件得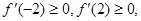
即 ∴-2≤a≤2.
∴-2≤a≤2.
所以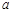 的取值范围为[-2,2]. ……………………………………12分
的取值范围为[-2,2]. ……………………………………12分
解法二:令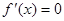 即
即 由求根公式得:
由求根公式得: 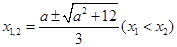
所以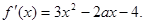 在
在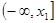 和
和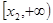 上非负.
上非负.
由题意可知,当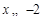 或
或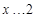 时,
时, 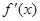 ≥0,
≥0,
从而 ,
, 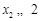 ,
,
即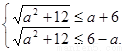 解不等式组得-2≤
解不等式组得-2≤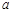 ≤2.
≤2.
∴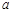 的取值范围是
的取值范围是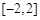 .
.
考点:函数求导数求最值判定单调性
点评:函数最值一般出现在极值点或线段端点处,根据导函数图像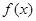 在
在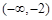 和
和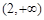 上都是递增的可得函数的导数
上都是递增的可得函数的导数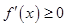 ,解法一利用数形结合法,利用导函数图像求解较简单
,解法一利用数形结合法,利用导函数图像求解较简单

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
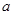 为实数,
为实数,
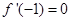 ,求
,求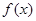 在
在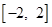 上最大值和最小值;
上最大值和最小值;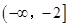 和
和 上都是递增的,求
上都是递增的,求 为实数.
为实数. ,求
,求 ;
; ,求
,求 ,
, 的值.
的值. 为实数,
为实数, (1)求导数
(1)求导数 ;(2)若
;(2)若 ,求
,求 在
在 上的最大值和最小值
上的最大值和最小值