题目内容
二项式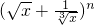 的展开式的各项系数和为64,则展开式中系数最大的项是________.
的展开式的各项系数和为64,则展开式中系数最大的项是________.

分析:令x=1,可求出展开式中的各项系数之和,由已知求出n=6,注意到展开式中各项系数等于各项的二项式系数,故中间项即第4项系数最大,利用二项展开式的通项公式求出答案.
解答:由已知,令x=1,展开式中的各项系数之和为2n
∴2n=64
∴n=6.
展开式中各项系数等于各项的二项式系数,系数最大的项为第4项,
所以

故答案为:
 .
.点评:本题考查二项式定理的应用,考查赋值思想、求指定的项.属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
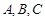 是表面积为
是表面积为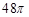 的球面
的球面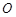 (
(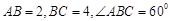 ,则三棱锥
,则三棱锥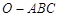 的体积为
的体积为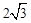 ;②二项式
;②二项式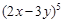 的展开式的各项的系数和为
的展开式的各项的系数和为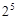 ;③已知函数
;③已知函数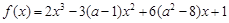 在
在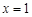 处取得极值,则实数
处取得极值,则实数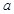 的值是
的值是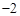 或
或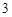 ;④已知点
;④已知点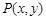 是抛物线
是抛物线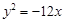 的准线与双曲线
的准线与双曲线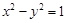 的两条渐近线所围成的三角形区域(含边界)内的任意一点,则
的两条渐近线所围成的三角形区域(含边界)内的任意一点,则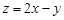 的最大值为9。其中正确命题的序号有__________
的最大值为9。其中正确命题的序号有__________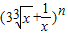 的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n=( )
的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n=( )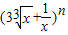 的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n=( )
的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n=( )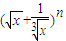 的展开式的各项系数和为64,则展开式中系数最大的项是 .
的展开式的各项系数和为64,则展开式中系数最大的项是 .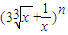 的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n=( )
的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n=( )