题目内容
（2013•福建）已知等差数列{an}的公差d=1，前n项和为Sn．
（I）若1，a1，a3成等比数列，求a1；
（II）若S5＞a1a9，求a1的取值范围．
（I）若1，a1，a3成等比数列，求a1；
（II）若S5＞a1a9，求a1的取值范围．
分析：（I）利用等差数列{an}的公差d=1，且1，a1，a3成等比数列，建立方程，即可求a1；
（II）利用等差数列{an}的公差d=1，且S5＞a1a9，建立不等式，即可求a1的取值范围．
（II）利用等差数列{an}的公差d=1，且S5＞a1a9，建立不等式，即可求a1的取值范围．
解答：解：（I）∵等差数列{an}的公差d=1，且1，a1，a3成等比数列，
∴a12=1×(a1+2)
∴a12-a1-2=0
∴a1=-1或a1=2；
（II）∵等差数列{an}的公差d=1，且S5＞a1a9，
∴5a1+10＞a12+8a1
∴a12+3a1-10＜0
∴-5＜a1＜2．
∴a12=1×(a1+2)
∴a12-a1-2=0
∴a1=-1或a1=2；
（II）∵等差数列{an}的公差d=1，且S5＞a1a9，
∴5a1+10＞a12+8a1
∴a12+3a1-10＜0
∴-5＜a1＜2．
点评：本题主要考查等差数列、等比数列、不等式等基础知识，考查运算能力，考查函数与方程思想，考查化归与转化思想，属于中档题．
练习册系列答案
相关题目
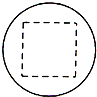（2013•福建）已知某一多面体内接于球构成一个简单组合体，如果该组合体的正视图、俯视图、均如图所示，且图中的四边形是边长为2的正方形，则该球的表面积是