题目内容
(2013•福建)已知函数f(x)=x-alnx(a∈R)
(1)当a=2时,求曲线y=f(x)在点A(1,f(1))处的切线方程;
(2)求函数f(x)的极值.
(1)当a=2时,求曲线y=f(x)在点A(1,f(1))处的切线方程;
(2)求函数f(x)的极值.
分析:(1)把a=2代入原函数解析式中,求出函数在x=1时的导数值,直接利用直线方程的点斜式写直线方程;
(2)求出函数的导函数,由导函数可知,当a≤0时,f′(x)>0,函数在定义域(0,+∝)上单调递增,函数无极值,当a>0时,求出导函数的零点,由导函数的零点对定义域分段,利用原函数的单调性得到函数的极值.
(2)求出函数的导函数,由导函数可知,当a≤0时,f′(x)>0,函数在定义域(0,+∝)上单调递增,函数无极值,当a>0时,求出导函数的零点,由导函数的零点对定义域分段,利用原函数的单调性得到函数的极值.
解答:解:函数f(x)的定义域为(0,+∞),f′(x)=1-
.
(1)当a=2时,f(x)=x-2lnx,f′(x)=1-
(x>0),
因而f(1)=1,f′(1)=-1,
所以曲线y=f(x)在点A(1,f(1))处的切线方程为y-1=-(x-1),
即x+y-2=0
(2)由f′(x)=1-
=
,x>0知:
①当a≤0时,f′(x)>0,函数f(x)为(0,+∞)上的增函数,函数f(x)无极值;
②当a>0时,由f′(x)=0,解得x=a.
又当x∈(0,a)时,f′(x)<0,当x∈(a,+∞)时,f′(x)>0.
从而函数f(x)在x=a处取得极小值,且极小值为f(a)=a-alna,无极大值.
综上,当a≤0时,函数f(x)无极值;
当a>0时,函数f(x)在x=a处取得极小值a-alna,无极大值.
| a |
| x |
(1)当a=2时,f(x)=x-2lnx,f′(x)=1-
| 2 |
| x |
因而f(1)=1,f′(1)=-1,
所以曲线y=f(x)在点A(1,f(1))处的切线方程为y-1=-(x-1),
即x+y-2=0
(2)由f′(x)=1-
| a |
| x |
| x-a |
| x |
①当a≤0时,f′(x)>0,函数f(x)为(0,+∞)上的增函数,函数f(x)无极值;
②当a>0时,由f′(x)=0,解得x=a.
又当x∈(0,a)时,f′(x)<0,当x∈(a,+∞)时,f′(x)>0.
从而函数f(x)在x=a处取得极小值,且极小值为f(a)=a-alna,无极大值.
综上,当a≤0时,函数f(x)无极值;
当a>0时,函数f(x)在x=a处取得极小值a-alna,无极大值.
点评:本题考查了利用导数研究曲线上某点处的切线方程,考查了利用导数研究函数的极值,考查了分类讨论得数学思想,属中档题.

练习册系列答案
 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
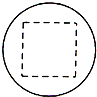 (2013•福建)已知某一多面体内接于球构成一个简单组合体,如果该组合体的正视图、俯视图、均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是
(2013•福建)已知某一多面体内接于球构成一个简单组合体,如果该组合体的正视图、俯视图、均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是