题目内容
已知f(x)=Asin(ωx+φ),其中A>0,ω>0,0≤?<2π.
(1)如图所示的是一个周期内的函数图象,试写出f(x)=Asin(ωx+φ)的解析式.
(2)如果在任意一段
内,f(x)能同时取得最大值A和最小值-A,那么正整数ω的最小值是多少?
(1)如图所示的是一个周期内的函数图象,试写出f(x)=Asin(ωx+φ)的解析式.

(2)如果在任意一段
| 1 | 150 |
分析:(1)结合三角函数的图象求出A,周期,过的平衡点,利用三角函数的周期公式求出ω,将平衡点的坐标代入整体角求出φ.
(2)将问题转化为三角函数的周期范围,利用周期公式求出ω的最小值.
(2)将问题转化为三角函数的周期范围,利用周期公式求出ω的最小值.
解答: 解:(1)由图知函数的最大值为300所以A=300
解:(1)由图知函数的最大值为300所以A=300
由图知函数的最小正周期为T=2(
+
)=
,
又T=
,ω=150π,
所以f(x)=300sin(150πx+φ);
∵f(x)=Asin(ωx+φ)过点(-
,0),
∴300sin(150π•(-
)+φ)=0.150π•(-
)+φ=0,∴φ=
.
f(x)=300sin(150πx+
);
(2)据题意知T≤
∴ω≥300π
ωmin=943.
∴正整数ω的最小值是943.
 解:(1)由图知函数的最大值为300所以A=300
解:(1)由图知函数的最大值为300所以A=300由图知函数的最小正周期为T=2(
| 1 |
| 180 |
| 1 |
| 900 |
| 1 |
| 75 |
又T=
| 2π |
| ω |
所以f(x)=300sin(150πx+φ);
∵f(x)=Asin(ωx+φ)过点(-
| 1 |
| 900 |
∴300sin(150π•(-
| 1 |
| 900 |
| 1 |
| 900 |
| π |
| 6 |
f(x)=300sin(150πx+
| π |
| 6 |
(2)据题意知T≤
| 1 |
| 150 |
∴ω≥300π
ωmin=943.
∴正整数ω的最小值是943.
点评:本题考查知三角函数的图象求解析式:其中A由图象的最值点求得;ω由周期确定;φ由特殊点确定.考查计算能力.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
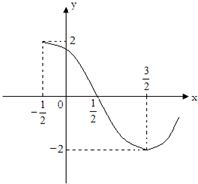 已知f(x)=Asin(ωπx+?)(A>0,ω>0,0<?<π),其导函数f′(x)的部分图象如图所示,则f(0)+f(1)+f(2)+f(3)+…f(2011)的值是( )
已知f(x)=Asin(ωπx+?)(A>0,ω>0,0<?<π),其导函数f′(x)的部分图象如图所示,则f(0)+f(1)+f(2)+f(3)+…f(2011)的值是( )A、-
| ||||
B、
| ||||
| C、1 | ||||
| D、0 |
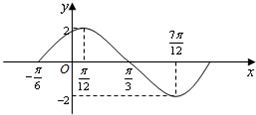 已知f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)图象的一部分如图所示:
已知f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)图象的一部分如图所示: