Question

利用“五点法”作出函数y=2sinx，x∈[0，2π]的简图，并回答下列问题．
（1）观察所作图象，写出满足条件sinx＞0的x的取值集合；
（2）利用函数单调性，求函数在区间(

π

4

，

5π

4

]上的最值，并写出取最值时对应的自变量x的取值．

Answer 1

分析：（1）用五点法作函数y=Asin（ωx+φ）的图象，结合函数y=Asin（ωx+φ）的图象特征，写出满足条件sinx＞0的x的取值集合．
（2）先求出函数的函数单区间，从而求得函数在区间(

π

4

，

5π

4

]上的最值，并写出取最值时对应的自变量x的取值．

解答：解：（1）列表：

x	0	π 2	π	3π 2	2π
2sinx	0	2	0	-2	0

图象如图所示：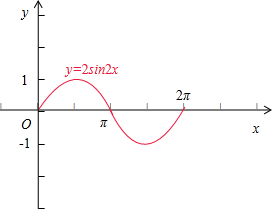
由图象可知，满足条件sinx＞0的x的取值集合为（0，π）．
（2）由图象可知，函数y=2sinx在(

π

4

，

π

2

]单调递增，在(

π

2

，

5π

4

]单调递减，
所以，当x=

π

2

时，f_max（x）=2；当x=

5π

4

时，fmin(x)=-

2

．

点评：本题主要考查用五点法作函数y=Asin（ωx+φ）的图象，函数y=Asin（ωx+φ）的图象特征，属于中档题．