题目内容
(本小题满分12分)
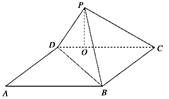
如图,在直四棱柱ABCD-A B
B C
C D
D 中,底面ABCD为等腰梯形,AB//CD,AB="4," BC="CD=2, " AA
中,底面ABCD为等腰梯形,AB//CD,AB="4," BC="CD=2, " AA ="2, " E、E
="2, " E、E 、F分别是棱AD、AA
、F分别是棱AD、AA 、AB的中点。
、AB的中点。
(1) 证明:直线EE
 //平面FCC
//平面FCC ;
;
(2) 求二面角B-FC -C的余弦值。
-C的余弦值。

如图,在直四棱柱ABCD-A
 B
B C
C D
D 中,底面ABCD为等腰梯形,AB//CD,AB="4," BC="CD=2, " AA
中,底面ABCD为等腰梯形,AB//CD,AB="4," BC="CD=2, " AA ="2, " E、E
="2, " E、E 、F分别是棱AD、AA
、F分别是棱AD、AA 、AB的中点。
、AB的中点。(1) 证明:直线EE

 //平面FCC
//平面FCC ;
;(2) 求二面角B-FC
 -C的余弦值。
-C的余弦值。 
(1)在直四棱柱ABCD-A
 B
B C
C D
D 中,取A1B1的中点F1,
中,取A1B1的中点F1,
连接A1D,C1F1,CF1,因为AB="4," CD=2,且AB//CD,
所以CDA1F1,A1F1CD为平行四边形,所以CF1//A1D,
又因为E、E
 分别是棱AD、AA
分别是棱AD、AA 的中点,所以EE1//A1D,
的中点,所以EE1//A1D,所以CF1//EE1,又因为
 平面FCC
平面FCC ,
, 平面FCC
平面FCC ,
,所以直线EE
 //平面FCC
//平面FCC .
.(2)因为AB="4," BC="CD=2," 、F是棱AB的中点,所以BF=BC=CF,△BCF为正三角形,取CF的中点O,则OB⊥CF,又因为直四棱柱ABCD-A
 B
B C
C D
D 中,CC1⊥平面ABCD,所以CC1⊥BO,所以OB⊥平面CC1F,过O在平面CC1F内作OP⊥C1F,垂足为P,连接BP,则∠OPB为二面角B-FC
中,CC1⊥平面ABCD,所以CC1⊥BO,所以OB⊥平面CC1F,过O在平面CC1F内作OP⊥C1F,垂足为P,连接BP,则∠OPB为二面角B-FC -C的一个平面角, 在△BCF为正三角形中,
-C的一个平面角, 在△BCF为正三角形中, ,在Rt△CC1F中, △OPF∽△CC1F,∵
,在Rt△CC1F中, △OPF∽△CC1F,∵ ∴
∴ ,
,在Rt△OPF中,
 ,
, ,所以二面角B-FC
,所以二面角B-FC -C的余弦值为
-C的余弦值为 .
.略

练习册系列答案
相关题目




 中,
中,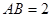 ,
,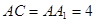 ,
,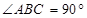 .
.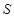 ;
;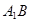 与
与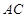 所成角的大小(结果用反三角函数表示).
所成角的大小(结果用反三角函数表示).
 ,则下列推论中正确的是( )
,则下列推论中正确的是( ) ,则
,则
 ,b//
,b// 共面,则
共面,则
 ,则a//b
,则a//b 中,与直线
中,与直线 异面,且与
异面,且与 的面对角线共有 条.
的面对角线共有 条.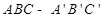 的正(主)视图和侧(左)视图如图所示. 设
的正(主)视图和侧(左)视图如图所示. 设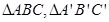 的中心分别是
的中心分别是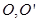 ,现将此三棱柱绕直线
,现将此三棱柱绕直线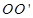 旋转,射线
旋转,射线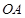 旋转所成的角为
旋转所成的角为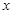 弧度(
弧度(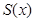 ,则函数
,则函数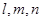 为两两不重合的直线,
为两两不重合的直线,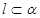 ,则
,则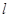 ∥
∥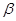
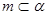 ,
,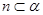 ,
,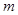 ∥β,
∥β,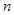 ∥β,则α∥β;
∥β,则α∥β;