题目内容
已![]() 知函数
知函数 是函数
是函数![]() 的极值点。 (I)求实数a的值,并确定实数m的取值范围,使得函数
的极值点。 (I)求实数a的值,并确定实数m的取值范围,使得函数![]() 有两个零点; (II)是否存在这样的直线
有两个零点; (II)是否存在这样的直线![]() ,同时满足:①
,同时满足:①![]() 是函数
是函数![]() 的图象在点
的图象在点![]() 处的切线 ②
处的切线 ②![]() 与函数
与函数![]() 的图象相切于点
的图象相切于点![]() ,如果存在,求实数b的取值范围;不存在,请说明理由。
,如果存在,求实数b的取值范围;不存在,请说明理由。
解:(I)![]() [来源:学。科。网]
[来源:学。科。网]
![]()
由已知,![]()
![]()
得a=1 所以![]()
![]()
令![]()
当![]() 时
时
| x |
|
|
|
|
| - | 0 | + |
|
|
| 极小值 |
|
所以,当![]() 时,
时,![]() 单调递减,
单调递减,![]()
当![]()
![]()
要使函数![]() 有两个零点,即方程
有两个零点,即方程![]() 有两不相等的实数根,也即函数
有两不相等的实数根,也即函数![]() 的图象与直线
的图象与直线![]() 有两个不同的交点。
有两个不同的交点。
(1)当![]() 时,m=0或
时,m=0或![]()
(2)当b=0时,![]()
(3)当![]()
(II)假设存在,
![]() 时,
时,![]()
![]()
函数![]() 的图象在点
的图象在点![]() 处的切线
处的切线![]() 的方程为:
的方程为:![]()
![]() 直
直![]() 线
线![]() 与函数
与函数![]() 的图象相切于点
的图象相切于点![]() ,
,
![]()
![]() ,所以切线
,所以切线![]() 的斜率为
的斜率为![]()
所以切线![]() 的方程为
的方程为![]() [来源:Z.xx.k.Com]
[来源:Z.xx.k.Com]
即![]() 的方程为:
的方程为:![]()
得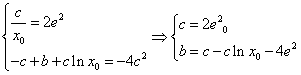 [来源:学_科_网Z_X_X_K]
[来源:学_科_网Z_X_X_K]
得![]() 其中
其中![]()
记![]() 其中
其中![]()
![]()
令![]()
|
|
| 1 |
|
|
| + | 0 | - |
|
|
| 极大值 |
|
又![]()
![]()
![]() KS5U
KS5U
所以实数b的取值范围的集合:![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知函数f(x)的定义域为[-1,5],部分对应值如下表.
已知函数f(x)的定义域为[-1,5],部分对应值如下表. 已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示,给出关于f(x)的下列命题:
已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示,给出关于f(x)的下列命题: 是函数
是函数 的图像上的两点,若对于任意实数
的图像上的两点,若对于任意实数 ,当
,当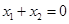 时,以
时,以 为切点分别作函数
为切点分别作函数 的图像的切线,则两切线必平行,并且当
的图像的切线,则两切线必平行,并且当 时函数
时函数 是函数
是函数 的图像上的一点,过
的图像上的一点,过 作函数
作函数 图像的切线,切线与
图像的切线,切线与 轴和直线
轴和直线 分别交于
分别交于 两点,直线
两点,直线 点,求△ABC的面积的最大值.
点,求△ABC的面积的最大值.