题目内容
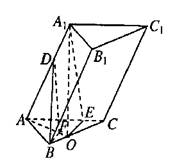
(12分)在三棱柱ABC―A1B1C1中底面是边长为2![]() 的正三角形,点A1在底面ABC上射影O
的正三角形,点A1在底面ABC上射影O
恰是BC的中点。
(1)求证:A1A⊥BC;
(2)当侧棱AA1和底面成45°角时,求二面角A―AC―B的
(3)若D为侧棱AA1上一点,当![]() 为何值时,BD⊥A1C1。
为何值时,BD⊥A1C1。

解析:解法一:(1)连接AO,∴AO1⊥面ABC,AO⊥BC. ∴A1A⊥BC。 ??4分
(2)由(1)得∠A1AO=45°
由底面是边长为2![]() 的正三角形,
的正三角形,
可知AO=3
∴A1O=3,AA1=3![]()
过O作OE⊥AC于E,连接A1E,
则∠A1EO为二面角A1―AC―B ????6分
∵![]() ∴tan∠A1EO=
∴tan∠A1EO=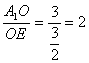 ???7分
???7分
即二面![]() 角A1―AC―B的大小为arctan2. ???8分
角A1―AC―B的大小为arctan2. ???8分
(3)过D作DF∥A1O,交AO于F,则DF⊥平面ABC,
∴BC为BD在面ABC内的射影,
又∵A1C1∥AC,∴要使BD⊥A1C1,只要BD⊥AC,即证BF⊥AC,
∴F为△ABC的中心,
∴![]() ???12分
???12分
解法二:以O为原点,OC为x轴,OA为y轴,OA1为z轴建立空间直角坐标系。
(1)由题意知∠A1AO=45°,A1O=3
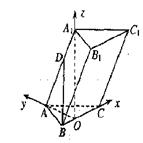
∴O(0,0,0)C(![]() ,0,0),A(0,3,0),A1(0,0,3),B(
,0,0),A(0,3,0),A1(0,0,3),B(![]() ,0,0)
,0,0)
∵![]() (0,-3,3),
(0,-3,3),![]() =(2
=(2![]() ,0,0)
,0,0)
∴![]()
∴AA1⊥BC ????4分
(2)设面ACA1的法向量为![]()
则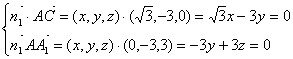
令z=1,则x=![]() ,y=1, ∴
,y=1, ∴![]() =(
=(![]() ,1,1) ????5分
,1,1) ????5分
而面ABC的法向量为![]() =(0,0,1)(6分)
=(0,0,1)(6分)
cos(![]() ,
,![]() )=
)=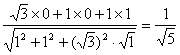
又显然所求二面角的平面角为锐角,
∴所求二面角的大小为arccos![]() ???8分
???8分
(3)A1C1∥AC,故只需BD⊥AC即可,设AD=a,则D(0,![]() ,
,![]() )
)
又B(![]() ,0,0),则
,0,0),则![]() (
(![]() ,
,![]() ,
,![]() ),
),![]() (
(![]() ,-3,0)。
,-3,0)。
要使BD⊥AC,须![]()

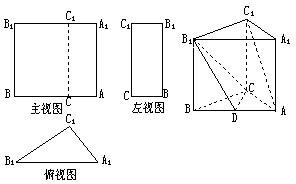 已知三棱柱ABC-A1B1C1的三视图如图所示,其中主视图AA1B1B和左视图B1BCC1均为矩形,在俯视图△A1B1C1中,A1C1=3,A1B1=5,
已知三棱柱ABC-A1B1C1的三视图如图所示,其中主视图AA1B1B和左视图B1BCC1均为矩形,在俯视图△A1B1C1中,A1C1=3,A1B1=5, 如图:在正三棱柱ABC-A1 B1 C1中,AB=
如图:在正三棱柱ABC-A1 B1 C1中,AB= 在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
在三棱柱ABC-A1B1C1中,已知AB=AC=AA1= (2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
(2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1= (2013•北京)如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
(2013•北京)如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.