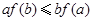题目内容
设 在区间
在区间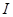 上有定义, 若
上有定义, 若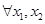
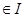 , 都有
, 都有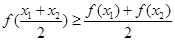 , 则称
, 则称 是区间
是区间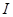 的向上凸函数;若
的向上凸函数;若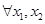
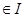 , 都有
, 都有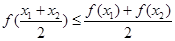 , 则称
, 则称 是区间
是区间 的向下凸函数. 有下列四个判断:
的向下凸函数. 有下列四个判断:
①若 是区间
是区间 的向上凸函数,则
的向上凸函数,则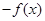 是区间
是区间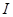 的向下凸函数;
的向下凸函数;
②若 和
和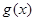 都是区间
都是区间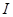 的向上凸函数, 则
的向上凸函数, 则 是区间
是区间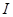 的向上凸函数;
的向上凸函数;
③若 在区间
在区间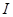 的向下凸函数且
的向下凸函数且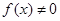 ,则
,则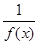 是区间
是区间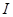 的向上凸函数;
的向上凸函数;
④若 是区间
是区间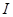 的向上凸函数,
的向上凸函数,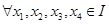 , 则有
, 则有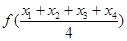
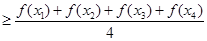
其中正确的结论个数是( )
| A.1 | B.2 | C.3 | D.4 |
①②
解析试题分析:利用定义易知正确,③反例 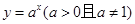
因为 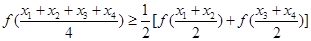
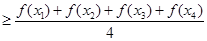 所以④正确.故填写①②。
所以④正确.故填写①②。
考点:函数的性质
点评:主要是对于新定义的理解和运用,属于中档题。

练习册系列答案
相关题目
已知R上可导函数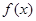 的图象如图所示,则不等式
的图象如图所示,则不等式 的解集为
的解集为
A.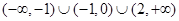 | B. |
C.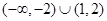 | D.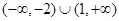 |
若定义在 上的函数
上的函数 满足:对任意
满足:对任意 ,有
,有 ,则下列说法一定正确的是( )
,则下列说法一定正确的是( )
A. 为奇函数 为奇函数 | B. 为偶函数 为偶函数 |
C. 为奇函数 为奇函数 | D. 为偶函数 为偶函数 |
若函数 的零点与
的零点与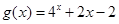 的零点之差的绝对值不超过
的零点之差的绝对值不超过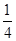 ,则
,则 可以是
可以是
A. =4x-1 =4x-1 | B. =(x-1)2 =(x-1)2 |
C. =ex-2 =ex-2 | D.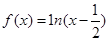 |
若函数f(x)=x3-12x在区间(k-1,k+1)上不是单调函数,则实数k的取值范围是( )
| A.k≤-3或-1≤k≤1或k≥3 | B.-3<k<-1或1<k<3 |
| C.-2<k<2 | D.不存在这样的实数 |
函数 是【 】.
是【 】.
A.最小正周期为 的奇函数 的奇函数 | B.最小正周期为 的奇函数 的奇函数 |
C.最小正周期为 的偶函数 的偶函数 | D.最小正周期为 的偶函数 的偶函数 |
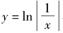 与.
与.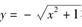 在同一平面直角坐标系内的大致图象为( )
在同一平面直角坐标系内的大致图象为( )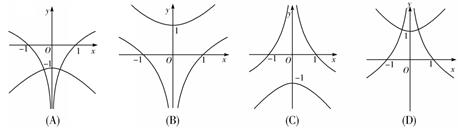
 是定义在
是定义在 上的非负可导函数,且满足
上的非负可导函数,且满足 ,对任意正数
,对任意正数 ,若
,若 ,则必有( )
,则必有( )