题目内容
 如图2-20,两个全等的正方形ABCD和ABEF所在平面相交于AB,M∈AC,N∈FB,且AM=FN,求证:MN//平面BCE。
如图2-20,两个全等的正方形ABCD和ABEF所在平面相交于AB,M∈AC,N∈FB,且AM=FN,求证:MN//平面BCE。
解析:
要证MN//平面BCE,就是要在平面BCE上找一条直线,证明它与MN平行即可。
证明: 连结AN并延长,交BE延长张于G,连结CG。
由AF//BG,知![]() ,故MN//CG,MN
,故MN//CG,MN![]() 平面BCE,CG
平面BCE,CG![]() 平面BCE,于是MN//平面BCE。
平面BCE,于是MN//平面BCE。
 点评:证线面平行,通常转化为证线线平行,关键是在平面内找到所需的线。
点评:证线面平行,通常转化为证线线平行,关键是在平面内找到所需的线。

练习册系列答案
相关题目
 某区组织群众性登山健身活动,招募了N名师生志愿者,将所有志愿者现按年龄情况分为15~20,20~25,25~30,30~35,35~40,40~45等六个层次,其频率分布直方图如图所示:已知30~35之间的志愿者共8人.
某区组织群众性登山健身活动,招募了N名师生志愿者,将所有志愿者现按年龄情况分为15~20,20~25,25~30,30~35,35~40,40~45等六个层次,其频率分布直方图如图所示:已知30~35之间的志愿者共8人.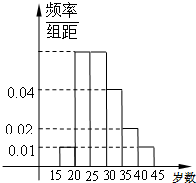 某单位组织群众性登山健身活动,招募了N名师生志愿者,将所有志愿者现按年龄情况分为15-20,20-25,25-30,30-35,35-40,40-45等六个层次,其频率分布直方图如图所示:已知30-35之间的志愿者共8人.
某单位组织群众性登山健身活动,招募了N名师生志愿者,将所有志愿者现按年龄情况分为15-20,20-25,25-30,30-35,35-40,40-45等六个层次,其频率分布直方图如图所示:已知30-35之间的志愿者共8人. ;
;