题目内容
设函数
(1)证明 当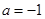 ,
,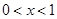 时,
时,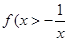 ;
;
(2)讨论 在定义域内的零点个数,并证明你的结论.
在定义域内的零点个数,并证明你的结论.
(1)见解析;(2)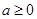 时
时 有唯一零点
有唯一零点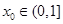 ,
,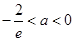 时,
时, 有两个零点
有两个零点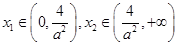 ,
,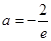 时
时 有唯一零点
有唯一零点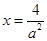 ,
,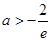 时
时 无零点.
无零点.
解析试题分析:(1)构造新函数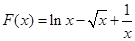 后证明
后证明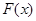 >0恒成立即可;(2)当
>0恒成立即可;(2)当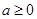 时通过单调性可知零点只有一个,当
时通过单调性可知零点只有一个,当 时通过
时通过 的最大值与0的比较即可判断零点情况.
的最大值与0的比较即可判断零点情况.
试题解析:(1)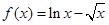 ,令
,令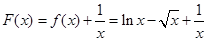 ,
,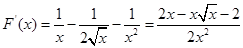 ,令
,令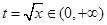 ,则令
,则令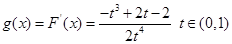 ,令
,令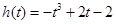 ,
,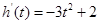 .
.
令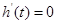 得
得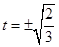 .当
.当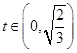 时
时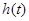 单调递增,
单调递增, 时
时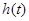 单调递减,
单调递减,
又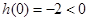 ,
,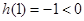 ,∴
,∴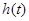 在
在 上恒小于零.即当
上恒小于零.即当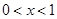 时
时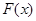 单调递减.
单调递减.
又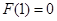 ,∴当
,∴当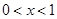 时,
时,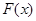 >0恒成立,即
>0恒成立,即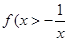 .
.
(2)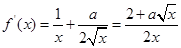 .
.
1°当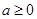 时,
时,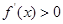 恒成立,即
恒成立,即 单调递增,此时
单调递增,此时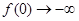 ,
,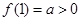 ,此时
,此时 的零点在
的零点在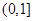 上.
上.
2°当 时,
时,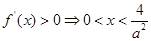 ,
,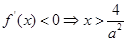 .
.
∴ 在
在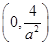 上单调递增,在
上单调递增,在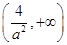 上单调递减,∴
上单调递减,∴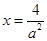 为
为 的最大值点.
的最大值点.
令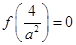 可得
可得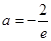 即当
即当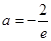 时
时 有唯一零点
有唯一零点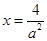 ;
;
当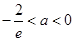 时,
时,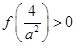 ,此时
,此时 有两个零点
有两个零点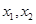 ,
,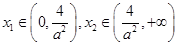 ;
;
当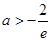 时,
时, ,∴
,∴ 在
在 上无零点.
上无零点.
综上所述,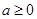 时
时 有唯一零点
有唯一零点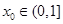 ,
,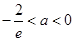 时,
时, 有两个零点
有两个零点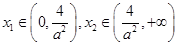 ,
,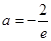 时
时 有唯一零点
有唯一零点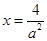 ,
,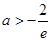 时
时 无零点.
无零点.
考点:1.导数证明不等式;2.函数的零点;3函数的单调性和最值.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
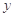 (单位:千克)与销售价格
(单位:千克)与销售价格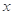 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式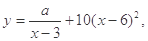 其中
其中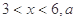 为常数.己知销售价格为5元/千克时,每日可售出该商品11千克.
为常数.己知销售价格为5元/千克时,每日可售出该商品11千克.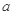 的值;
的值;
 .
. 的单调递增区间;
的单调递增区间; ,函数
,函数 上都有三个零点,求实数
上都有三个零点,求实数 的取值范围.
的取值范围.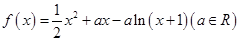 .
.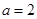 时,求函数
时,求函数 的极值;
的极值;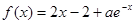 (
(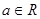 )
)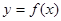 在点
在点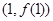 处的切线平行于
处的切线平行于 轴,求
轴,求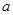 的值;
的值;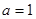 时,若直线
时,若直线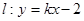 与曲线
与曲线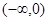 上有公共点,求
上有公共点,求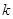 的取值范围.
的取值范围.

 在
在 处的切线垂直
处的切线垂直 轴,求
轴,求 的值;
的值; 上为增函数,求
上为增函数,求 的单调性.
的单调性.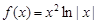 ,
, 的奇偶性;
的奇偶性; 的方程
的方程 有实数解,求实数
有实数解,求实数 的取值范围
的取值范围  ,
, 的单调性;
的单调性; ,则对于任意
,则对于任意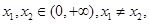 有
有 。
。
 )处的切线方程
)处的切线方程 的单调递增区间
的单调递增区间