题目内容
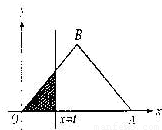
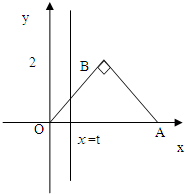 如图,△OAB是斜边长为4的等腰直角三角形,记△OAB位于直线x=t(0≤t≤4)左侧的图形的面积为f(t).
如图,△OAB是斜边长为4的等腰直角三角形,记△OAB位于直线x=t(0≤t≤4)左侧的图形的面积为f(t).
(1)求函数f(t)的解析式及f(1)的值;
(2)若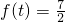 时,求t的值.
时,求t的值.
解:(1)当0<t≤2时,
如图,设直线x=t与△OAB的OA,OB分别交于C、D两点,
因为△OAB是斜边长为4的等腰直角三角形,并且|OC|=t,
所以|CD|=t.
f(t)= |OC|•|CD|=
|OC|•|CD|= •t•t=
•t•t= t2.
t2.
当2<t≤4时,设直线x=t与△OAB的AB,OA分别交于M、N两点,则|AN|=4-t,
因为△OAB是斜边长为4的等腰直角三角形,
所以△OAB的面积为:S△OAB= ×4×2=4.
×4×2=4.
又因为|AN|=4-t,
所以|MN|=4-t.
所以f(t)=4- •|AN|•|MN|=4-
•|AN|•|MN|=4- (4-t)2=-
(4-t)2=- t2+4t-4.
t2+4t-4.
所以f(t)= .
.
∴f(1)= ;
;
(2)若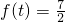 ,由(1)可得:
,由(1)可得:
当0<t≤2时,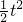 =
= ,∴t∈∅;
,∴t∈∅;
当2<t≤4时,- t2+4t-4=
t2+4t-4= ,∴t=3.
,∴t=3.
综上,t=3.
分析:(1)求f(t)的解析式时,关键是要根据图象,对t的取值进行恰当的分段,然后分段求出函数的解析式.
(2)结合分段函数的解析式,再利用分类讨论即可求出t的值.
点评:解决分段函数的问题时,首先要确定自变量的数值属于哪一个区间段,从而选相应的关系式,对于分段函数,注意处理好各段的端点,分段函数的图象也是分段进行.
如图,设直线x=t与△OAB的OA,OB分别交于C、D两点,
因为△OAB是斜边长为4的等腰直角三角形,并且|OC|=t,
所以|CD|=t.
f(t)=
 |OC|•|CD|=
|OC|•|CD|= •t•t=
•t•t= t2.
t2.当2<t≤4时,设直线x=t与△OAB的AB,OA分别交于M、N两点,则|AN|=4-t,
因为△OAB是斜边长为4的等腰直角三角形,
所以△OAB的面积为:S△OAB=
 ×4×2=4.
×4×2=4.又因为|AN|=4-t,
所以|MN|=4-t.
所以f(t)=4-
 •|AN|•|MN|=4-
•|AN|•|MN|=4- (4-t)2=-
(4-t)2=- t2+4t-4.
t2+4t-4.所以f(t)=
 .
.∴f(1)=
 ;
;(2)若
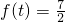 ,由(1)可得:
,由(1)可得:当0<t≤2时,
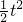 =
= ,∴t∈∅;
,∴t∈∅;当2<t≤4时,-
 t2+4t-4=
t2+4t-4= ,∴t=3.
,∴t=3.综上,t=3.
分析:(1)求f(t)的解析式时,关键是要根据图象,对t的取值进行恰当的分段,然后分段求出函数的解析式.
(2)结合分段函数的解析式,再利用分类讨论即可求出t的值.
点评:解决分段函数的问题时,首先要确定自变量的数值属于哪一个区间段,从而选相应的关系式,对于分段函数,注意处理好各段的端点,分段函数的图象也是分段进行.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 如图,△OAB是斜边长为4的等腰直角三角形,记△OAB位于直线x=t(0≤t≤4)左侧的图形的面积为f(t).
如图,△OAB是斜边长为4的等腰直角三角形,记△OAB位于直线x=t(0≤t≤4)左侧的图形的面积为f(t). 如图,△OAB是斜边长为4的等腰直角三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t).
如图,△OAB是斜边长为4的等腰直角三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t).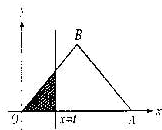 如图,△OAB是斜边长为4的等腰直角三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t).
如图,△OAB是斜边长为4的等腰直角三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t).