题目内容
在四棱锥P—ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成角为60°.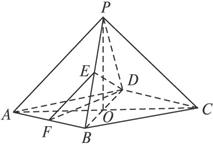
(1)求四棱锥P—ABCD的体积;
(2)若E是PB的中点,求异面直线DE与PA所成角的大小(结果用反三角函数值表示).
解:(1)在四棱锥P—ABCD中,由PO⊥平面ABCD,得∠PBO是PB与平面ABCD所成角,∠PBO=60°.
在Rt△AOB中,BO=ABsin30°=1,又PO⊥BO,于是,PO=BOtan60°=![]() ,而底面菱形的面积SABCD=
,而底面菱形的面积SABCD=![]() ,
,
∴四棱锥P—ABCD的体积VP—ABCD=![]() ×
×![]() ×
×![]() =2.
=2.
(2)取AB的中点F,连结EF、DF.

由E是PB的中点,得EF∥PA,
∴∠FED是异面直线DE与PA所成角(或它的补角).
在Rt△AOB中,OA=ABcos30°=![]() =OP,于是,在等腰直角△POA中,PA=
=OP,于是,在等腰直角△POA中,PA=![]() ,则EF=
,则EF=![]() .
.
而在正△ABD和正△PBD中,DE=DF=![]() .
.
cos∠FED=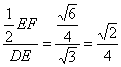 ,
,
∴异面直线DE与PA所成角的大小是arccos![]() .
.

练习册系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M,N分别为PC、PB的中点.
如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M,N分别为PC、PB的中点. 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4.AB=2,AN⊥PC于点N,M是PD中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4.AB=2,AN⊥PC于点N,M是PD中点. 如图,在四棱锥P-ABCD中,底面ABCD是矩形,O为底面中心,PA⊥平面ABCD,PA=AD=2AB.M是PD的中点
如图,在四棱锥P-ABCD中,底面ABCD是矩形,O为底面中心,PA⊥平面ABCD,PA=AD=2AB.M是PD的中点 如图,在四棱锥P-ABCD中,底面ABCD是矩形,已知AB=3,AD=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形,已知AB=3,AD=2,PA=2,PD=2 (2009•成都模拟)如图,在四棱锥P-ABCD中,底面ABCD为正方形,且PD⊥平面ABCD,PD=AB=1,EF分别是PB、AD的中点,
(2009•成都模拟)如图,在四棱锥P-ABCD中,底面ABCD为正方形,且PD⊥平面ABCD,PD=AB=1,EF分别是PB、AD的中点,