题目内容
已知向量 =(
=( x,x-4),向量
x,x-4),向量 =(x,
=(x, x),x∈[-4,5]
x),x∈[-4,5]
(Ⅰ)试用x表示 •
• ;
;
(Ⅱ)求 •
• 的最大值,并求此时的cos<
的最大值,并求此时的cos< 、
、 >.(<
>.(< 、
、 >表示两向量的夹角)
>表示两向量的夹角)
解:(Ⅰ) •
• =2x2-6x-----------------------------------------(3分)
=2x2-6x-----------------------------------------(3分)
(Ⅱ)设f(x)=2x2-6x=2(x- )2-
)2- ,
,
∵x∈[-4,5]
∴当x=-4时, •
• 的最大值为56--------------------------------------(9分)
的最大值为56--------------------------------------(9分)
此时, =(-2,-8),
=(-2,-8), =(-4,-6),|
=(-4,-6),| |=
|=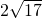 ,|
,| |=2
|=2
设 、
、 的夹角为θ,则cosθ=
的夹角为θ,则cosθ= .------------------(12分)
.------------------(12分)
分析:(Ⅰ)直接利用斜率的数量积,求出 •
• 的表达式即可;
的表达式即可;
(Ⅱ)利用 •
• 的表达式,通过二次函数求出最大值,求出此时的cos<
的表达式,通过二次函数求出最大值,求出此时的cos< ,
, >的值.
>的值.
点评:本题考查向量的数量积与二次函数的最值的求法,考查计算能力.
 •
• =2x2-6x-----------------------------------------(3分)
=2x2-6x-----------------------------------------(3分)(Ⅱ)设f(x)=2x2-6x=2(x-
 )2-
)2- ,
,∵x∈[-4,5]
∴当x=-4时,
 •
• 的最大值为56--------------------------------------(9分)
的最大值为56--------------------------------------(9分)此时,
 =(-2,-8),
=(-2,-8), =(-4,-6),|
=(-4,-6),| |=
|=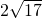 ,|
,| |=2
|=2
设
 、
、 的夹角为θ,则cosθ=
的夹角为θ,则cosθ= .------------------(12分)
.------------------(12分)分析:(Ⅰ)直接利用斜率的数量积,求出
 •
• 的表达式即可;
的表达式即可; (Ⅱ)利用
 •
• 的表达式,通过二次函数求出最大值,求出此时的cos<
的表达式,通过二次函数求出最大值,求出此时的cos< ,
, >的值.
>的值.点评:本题考查向量的数量积与二次函数的最值的求法,考查计算能力.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目