题目内容

设n=9
∫
π
2
0
sinxdx，则二项式(2x+
1
x
)a展开式中常数项是
672
672
（填数字）．
分析：利用微积分基本定理求出a，利用二项展开式的通项公式求出通项，令x的指数等于0，求出常数项．
解答：解：a=9
∫
π
2
0
sinxdx=-9cosx|0 
π
2
=9，
∴(2x+
1
x
)9展开式的通项为Tr+1=29-rC9rx 9-
3
2
r
令9-
3
2
r=0得r=6
故展开式的常数项是8C96=672．
故答案为：672．
点评：本题考查微积分基本定理、二项展开式的通项公式解决二项展开式的特定项问题，属于基础题．
练习册系列答案
相关题目
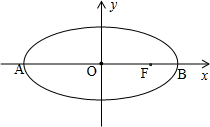精英家教网在平面直角坐标系xoy中，如图，已知椭圆
x2
9
+
y2
5
=1的左、右顶点为A、B，右焦点为F．设过点T（t，m）的直线TA、TB与椭圆分别交于点M（x1，y1）、N（x2，y2），其中m＞0，y1＞0，y2＜0．
（1）设动点P满足PF2-PB2=4，求点P的轨迹；
（2）设x1=2，x2=
1
3
，求点T的坐标；
（3）设t=9，求证：直线MN必过x轴上的一定点（其坐标与m无关）．
（2013•杭州一模）设等差数列{an}满足：
sin2a3-cos2a3+cos2a3cos2a6-sin2a3sin2a6
sin(a4+a5)
=1，公差d∈（-1，0）．若当且仅当n=9时，数列{an}的前n项和Sn取得最大值，则首项a1取值范围是（　　）
已知数集序列{1}，{3，5}，{7，9，11}，{13，15，17，19}，…，其中第n个集合有n个元素，每一个集合都由连续正奇数组成，并且每一个集合中的最大数与后一个集合中的最小数是连续奇数．
（1）求第n个集合中各数之和Sn的表达式；
（2）设n是不小于2的正整数，f(n)=
n
i=1
1
3Si
，求证：n+
n-1
i=1
f(i)=nf(n)．
设n=9
∫
π
2
0
sinxdx，则二项式(2x+
1
x
)a展开式中常数项是______（填数字）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网