题目内容
13.复数z满足i•z=1+i,其中i为虚数单位,则在复平面上复数z对应的点位于( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 利用复数的运算法则、几何意义即可得出.
解答 解:∵i•z=1+i,∴-i•i•z=-i(1+i),
∴z=1-i,
∴在复平面上复数z对应的点(1,-1)位于第四象限.
故选:D.
点评 本题考查了复数的运算法则、几何意义,属于基础题.

练习册系列答案
相关题目
1.四棱锥S-ABCD中,底面ABCD是边长为2$\sqrt{3}$的正方形,SA⊥平面ABCD,且SA=2$\sqrt{6}$,则此四棱锥的外接球的表面积为( )
| A. | 12π | B. | 24π | C. | 144π | D. | 48π |
3.命题p:已知α⊥β,则?l?α,都有l⊥β;命题q:已知l∥α,则?m?α,使得l不平行于m(其中α、β是平面,l、m是直线),则下列命题中真命题的是( )
| A. | (¬p)∧(¬q) | B. | p∨(¬q) | C. | p∧(¬q) | D. | (¬p)∧q |
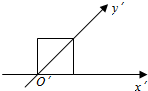 用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个边长为1的正方形,则原来的图形的面积是2$\sqrt{2}$.
用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个边长为1的正方形,则原来的图形的面积是2$\sqrt{2}$. 如图,C是圆O的直径AB上一点,CD⊥AB,与圆O相交于点D,与弦AF交于点E,与BF的延长线相交于点G.GT与圆相切于点T.
如图,C是圆O的直径AB上一点,CD⊥AB,与圆O相交于点D,与弦AF交于点E,与BF的延长线相交于点G.GT与圆相切于点T. 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为6.
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为6.