Question

1．四棱锥S-ABCD中，底面ABCD是边长为2$\sqrt{3}$的正方形，SA⊥平面ABCD，且SA=2$\sqrt{6}$，则此四棱锥的外接球的表面积为（　　）

• A． 12π
• B． 24π
• C． 144π
• D． 48π

Answer 1

分析 如图所示，连接AC，BD相交于点O₁．取SC的中点，连接OO₁．利用三角形的中位线定理可得OO₁∥SA．由于SA⊥底面ABCD，可得OO₁⊥底面ABCD．可得点O是四棱锥S-ABCD外接球的球心，SC是外接球的直径．

解答 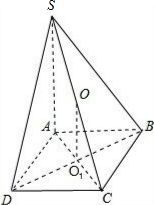解：如图所示
连接AC，BD相交于点O₁．取SC的中点，连接OO₁．
则OO₁∥SA．
∵SA⊥底面ABCD，
∴OO₁⊥底面ABCD．
可得点O是四棱锥S-ABCD外接球的球心．
因此SC是外接球的直径．
∵SC²=SA²+AC²=48．
∴四棱锥P-ABCD外接球的表面积为48π．
故选：D

点评 本题考查了线面垂直的性质、三角形的中位线定理、正方形的性质、勾股定理、球的表面积，考查了推理能力与计算能力，属于中档题．