题目内容
在边长为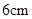 的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥.
的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥.
(I)判别MN与平面AEF的位置关系,并给出证明;
(II)求多面体E-AFMN的体积.
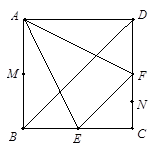
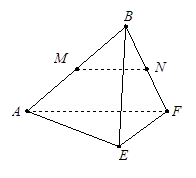
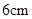 的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥.
的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥.(I)判别MN与平面AEF的位置关系,并给出证明;
(II)求多面体E-AFMN的体积.
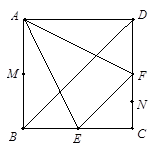
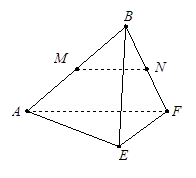
(1)见解析(2)

第一问因翻折后B、C、D重合(如下图),所以MN应是 的一条中位线,则利用线线平行得到线面平行。
的一条中位线,则利用线线平行得到线面平行。
第二问因为 平面BEF,……………8分
平面BEF,……………8分
且 ,
,
∴ ,又
,又 ∴
∴
(1)因翻折后B、C、D重合(如图),
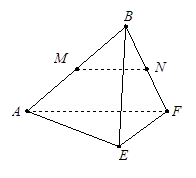
所以MN应是 的一条中位线,………………3分
的一条中位线,………………3分
则 .………6分
.………6分
(2)因为 平面BEF,……………8分
平面BEF,……………8分
且 ,
,
∴ ,………………………………………10分
,………………………………………10分
又 ∴
∴
 的一条中位线,则利用线线平行得到线面平行。
的一条中位线,则利用线线平行得到线面平行。第二问因为
 平面BEF,……………8分
平面BEF,……………8分且
 ,
,∴
 ,又
,又 ∴
∴
(1)因翻折后B、C、D重合(如图),
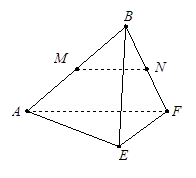
所以MN应是
 的一条中位线,………………3分
的一条中位线,………………3分则
 .………6分
.………6分(2)因为
 平面BEF,……………8分
平面BEF,……………8分且
 ,
,∴
 ,………………………………………10分
,………………………………………10分又
 ∴
∴

练习册系列答案
相关题目
 ,半径为3的球面上,且三棱锥
,半径为3的球面上,且三棱锥 B、
B、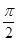 C、
C、 D、
D、

 被以A为球心,AB为半径的球相截,则所截得几何体(球内部分)的表面积为 ( )
被以A为球心,AB为半径的球相截,则所截得几何体(球内部分)的表面积为 ( )
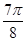


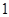
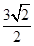
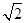
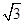
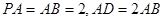 ,PA
,PA 平面ABCD, E,F分别是BC,PC的中点。
平面ABCD, E,F分别是BC,PC的中点。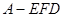 的体积。
的体积。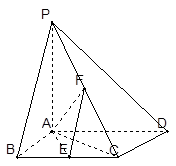
 的所有顶点都在球
的所有顶点都在球 的求面上,
的求面上, 是边长为
是边长为 的正三角形,
的正三角形, 为球
为球 ;则此棱锥的体积为( )
;则此棱锥的体积为( )



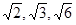 ,这个长方体它的八个顶点都在同一个球面上,这个球的表面积是( )
,这个长方体它的八个顶点都在同一个球面上,这个球的表面积是( )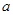
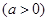 ,PA
,PA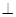 平面ABCD,且PA=1。
平面ABCD,且PA=1。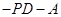 的正切。
的正切。