题目内容
如下图,在四棱柱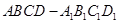 中,底面
中,底面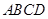 和侧面
和侧面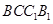 都
都
是矩形,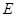 是
是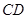 的中点,
的中点,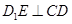 ,
,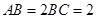 .
.
(1)求证:
(2)求证: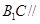 平面
平面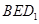 ;
;
(3)若平面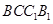 与平面
与平面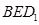 所成的锐二面角的大小为
所成的锐二面角的大小为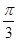 ,求线段
,求线段 的长度.
的长度.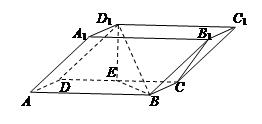

(1)详见解析;(2)详见解析;(3)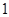 .
.
解析试题分析:(1)利用已知条件得到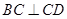 ,
,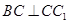 ,从而证明
,从而证明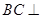 平面
平面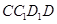 ,得到
,得到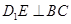 再结合
再结合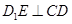 证明
证明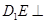 平面
平面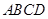 ,从而得到
,从而得到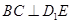 ;(2)连接
;(2)连接 、
、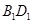 证明四边形
证明四边形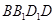 为平行四边形,连接对角线的交点与点
为平行四边形,连接对角线的交点与点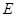 的连线为
的连线为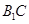 的中位线,再利用线面平行的判定定理即可证明
的中位线,再利用线面平行的判定定理即可证明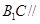 平面
平面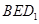 ;(3)在(1)的前提条件中
;(3)在(1)的前提条件中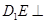 平面
平面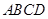 下,选择以点
下,选择以点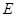 为坐标原点,
为坐标原点,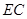 、
、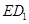 分别为
分别为 轴、
轴、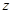 轴的空间直角坐标系,设
轴的空间直角坐标系,设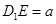 ,利用法向量将条件“平面
,利用法向量将条件“平面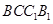 与平面
与平面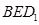 所成的锐二面角的大小为
所成的锐二面角的大小为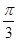 ”进行转化,从而求出
”进行转化,从而求出 的长度.
的长度.
试题解析:(1)因为底面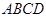 和侧面
和侧面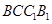 是矩形,
是矩形,
所以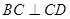 ,
,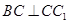 ,
,
又因为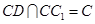 ,
,
所以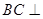 平面
平面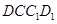 ,
,
因为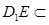 平面
平面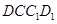 ,
,
所以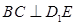 ;
;
(2)因为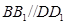 ,
,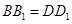 ,
,
所以四边形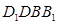 是平行四边形.
是平行四边形.
连接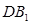 交
交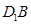 于点
于点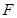 ,连接
,连接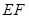 ,则
,则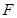 为
为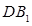 的中点.
的中点.
在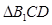 中,因为
中,因为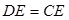 ,
,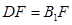 ,
,
所以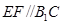 .
.
又因为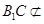 平面
平面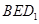 ,
,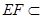 平面
平面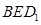 ,
,
所以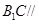 平面
平面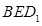 ;
;
(3)由(1)可知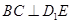 ,
,
又因为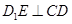 ,
,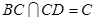 ,
,
所以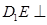 平面
平面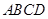 .
.
设G为AB的中点,以E为原点, 、
、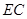 、
、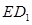 所在直线分别为
所在直线分别为 轴、
轴、 轴、
轴、
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,
中, 分别是棱
分别是棱 的中点,点
的中点,点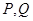 分别在棱
分别在棱 ,
,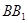 上移动,且
上移动,且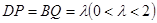 .
. 时,证明:直线
时,证明:直线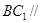 平面
平面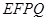 ;
; ,使平面
,使平面 所成的二面角为直二面角?若存在,求出
所成的二面角为直二面角?若存在,求出
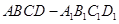 中,P是侧棱
中,P是侧棱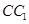 上的一点,
上的一点,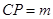 .
. 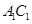 上是否存在一个定点
上是否存在一个定点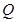 ,使得对任意的m,
,使得对任意的m,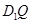 ⊥AP,并证明你的结论.
⊥AP,并证明你的结论. 
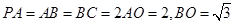 .
.
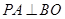 ;
; AB.Q是PC上的一点,且PA∥平面QBD.
AB.Q是PC上的一点,且PA∥平面QBD.
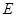 是以
是以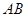 为直径的半圆
为直径的半圆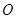 上异于
上异于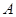 、
、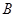 的点,矩形
的点,矩形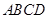 所在的平面垂直于半圆
所在的平面垂直于半圆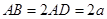 .
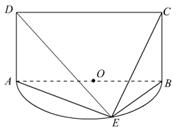
.
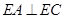 ;
;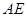 和
和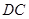 所成的角为
所成的角为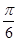 ,求平面
,求平面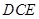 与平面
与平面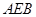 所成的锐二面角的余弦值.
所成的锐二面角的余弦值. 中,
中, 为
为 的中点,
的中点, ,
, ,
, .将此平面四边形
.将此平面四边形 折成直二面角
折成直二面角 ,
,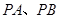 ,设
,设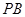 中点为
中点为 .
.
 平面
平面 ;
; 上是否存在一点
上是否存在一点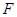 ,使得
,使得 平面
平面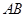 与平面
与平面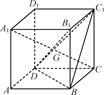
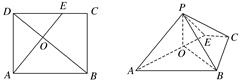
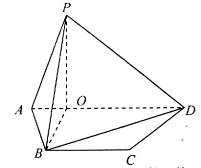
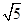 ,AD=6,BD是对角线,过点A作AE⊥BD,垂足为O,交CD于E,以AE为折痕将△ADE向上折起,使点D到点P的位置,且PB=
,AD=6,BD是对角线,过点A作AE⊥BD,垂足为O,交CD于E,以AE为折痕将△ADE向上折起,使点D到点P的位置,且PB=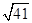 .
.