题目内容
已知函数f(x)=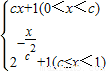 满足f(c2)=
满足f(c2)= .
.(1)求常数c的值;
(2)解不等式f(x)>
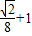 .
.
【答案】分析:(1)先判定c2的大小,从而断定代入哪一个解析式,建立等量关系,解之即可;
(2)根据分段函数的分类标准进行分类讨论,分别在每一段上求解不等式,注意解集与前提求交集,最后将两种情形求并集即可.
解答:解(1)依题意0<c<1,
∴c2<c,∵f(c2)= ,c=
,c=
(2)由(1)得f(x)=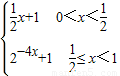
由f(x)>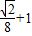 得
得
当0<x< 时,
时,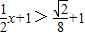 ∴
∴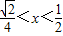
当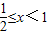 时,
时,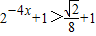 ,∴
,∴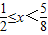
综上所述: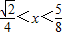
∴f(x)>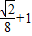 的解集为{x|
的解集为{x|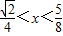 }
}
点评:本题主要考查了函数与方程的综合运用,以及不等式的解集问题,属于基础题.
(2)根据分段函数的分类标准进行分类讨论,分别在每一段上求解不等式,注意解集与前提求交集,最后将两种情形求并集即可.
解答:解(1)依题意0<c<1,
∴c2<c,∵f(c2)=
 ,c=
,c=
(2)由(1)得f(x)=
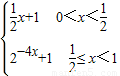
由f(x)>
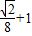 得
得当0<x<
 时,
时,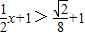 ∴
∴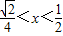
当
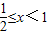 时,
时,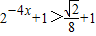 ,∴
,∴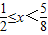
综上所述:
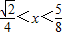
∴f(x)>
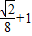 的解集为{x|
的解集为{x|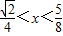 }
}点评:本题主要考查了函数与方程的综合运用,以及不等式的解集问题,属于基础题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
已知函数f(x)为R上的连续函数且存在反函数f-1(x),若函数f(x)满足下表:

那么,不等式|f-1(x-1)|<2的解集是( )

那么,不等式|f-1(x-1)|<2的解集是( )
A、{x|
| ||
B、{x|
| ||
| C、{x|1<x<2} | ||
| D、{x|1<x<5} |
 若数列{an}满a1=
若数列{an}满a1= ,an+1=f(an),n∈N*,则a2006+a2009+a2010= .
,an+1=f(an),n∈N*,则a2006+a2009+a2010= . 若数列{an}满a1=
若数列{an}满a1= ,an+1=f(an),n∈N*,则a2006+a2009+a2010= .
,an+1=f(an),n∈N*,则a2006+a2009+a2010= .
 <x<4}
<x<4} <x<3}
<x<3}