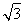题目内容
设f(x)=sin2x+acos2x的图象关于直线x=-
思路分析:因为函数的图象关于直线对称,所以有①直线x=-![]() 过图象的波峰或波谷(因原函数可化为正弦型函数y=
过图象的波峰或波谷(因原函数可化为正弦型函数y=![]() sin(2x+φ);②f(-
sin(2x+φ);②f(-![]() +x)=f(-
+x)=f(-![]() -x)对任何实数x恒成立.根据①或②有以下解法:
-x)对任何实数x恒成立.根据①或②有以下解法:
解法一:f(x)= ![]() sin(2x+φ),其中cosφ=
sin(2x+φ),其中cosφ=![]() ,sinφ=
,sinφ=![]() ,
,
又∵f(x)=sin2x+acos2x的图象关于x=-![]() 对称,
对称,
∴当x=-![]() 时,f(x)取最值.
时,f(x)取最值.
∴f(-![]() )=±
)=±![]() ,
,
即sin(-![]() )+acos(-
)+acos(-![]() )=
)=![]() (a-1)=±
(a-1)=±![]() ,两边平方,
,两边平方,
解得a=-1.
解法二:(特殊值法)
∵已知函数图象关于x=-![]() 对称,点(0,0)与(-
对称,点(0,0)与(-![]() ,0)关于x=-
,0)关于x=-![]() 对称,
对称,
∴f(0)=f(-![]() ),
),
即sin0+acos0=sin(-![]() )+acos(-
)+acos(-![]() ),
),
∴a=-1,而当a=-1时,f(x)=![]() sin(2x-
sin(2x-![]() ),x=-
),x=-![]() 是它的一条对称轴,
是它的一条对称轴,
故取a=-1.
解法三:(定义法)
∵图象关于x=-![]() 对称,
对称,
∴sin2(-![]() +x)+acos2(-
+x)+acos2(-![]() +x)
+x)
=sin2(-![]() -x)+acos2(-
-x)+acos2(-![]() -x),
-x),
∴2cos![]() sin2x=-2asin
sin2x=-2asin![]() sin2x,
sin2x,
∴a=-1.

练习册系列答案
相关题目
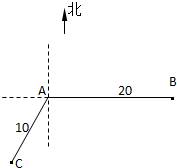 如图,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救、甲船立即前往救援,同时把消息告知在甲船的南偏西30°,相距10海里C处的乙船.
如图,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救、甲船立即前往救援,同时把消息告知在甲船的南偏西30°,相距10海里C处的乙船.