题目内容
设 在函数
在函数 的图像上,其中
的图像上,其中 是
是 的两个极值点,
的两个极值点, 是
是 的一个零点,若函数
的一个零点,若函数 的图像在
的图像在 处的切线与直线
处的切线与直线 垂直,则
垂直,则 .
.
【答案】

【解析】
试题分析:先把函数的零点求出来,再对函数f(x)求导并求出其零点,列出表格和画出图象,利用在斜率存在的条件下两条直线垂直的充要条件k1k2=-1即可求出答案。
令 =0,则有
=0,则有 ,因为
,因为 是
是 的一个零点,则可知
的一个零点,则可知 ,因为
,因为 ,结合导数的知识可知,函数在x=
,结合导数的知识可知,函数在x= 处取得极小值,则在x=
处取得极小值,则在x= 处取得极大值,然后根据函数
处取得极大值,然后根据函数

图像可知,当 时,函数
时,函数 则根据在点T 处的切线与AB直线垂直,可知a=
则根据在点T 处的切线与AB直线垂直,可知a= ;当
;当 时,函数
时,函数 则根据在点T 处的切线与AB直线垂直,可知a=
则根据在点T 处的切线与AB直线垂直,可知a= ,故综上可知,满足题意的a的取值为
,故综上可知,满足题意的a的取值为 。
。
考点:导数的运用
点评:充分利用导数研究函数的性质和理解函数的零点是解题的关键,属于中档题。

练习册系列答案
相关题目
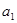 =2,点(
=2,点(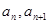 )在函数
)在函数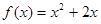 的图像上,其中
的图像上,其中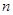 =
=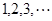 .
.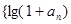 }是等比数列;
}是等比数列;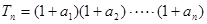 ,求
,求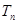 及数列{
及数列{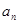 }的通项公式;
}的通项公式;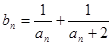 ,求数列{
,求数列{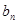 }的前n项和
}的前n项和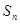 ,并证明
,并证明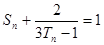 .
.  =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
.