题目内容
15．有一块以O点为圆心的半圆形空地，要在这块空地上划出一个内接矩形ABCD辟为绿地，使其一边AD落在半圆的直径上，另两点BC落在半圆的圆周上，已知半圆的半径长为a，如何选择关于点O对称的点A、D的位置，可以使矩形面积最大？分析 根据直角三角形中的三角函数和图形求出矩形的长和宽，再表示出矩形的面积，利用倍角的正弦公式化简，再由正弦函数的最值求出矩形面积的最大值．
解答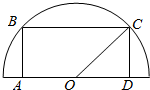 
解：令∠DOC=θ，DC=asinθ，AD=2acosθ
∴矩形ABCD的面积为S=AD•DC=2acosθ•asinθ=a2sin2θ，
当θ=$\frac{π}{4}$时，Smax=a2，
∴AD=$\sqrt{2}$a．
故使得OA=OD=$\frac{\sqrt{2}}{2}$a，划出的矩形的面积最大．
点评 本题是实际问题为背景，考查了倍角的正弦公式，以及直角三角形中的三角函数，注重数学在实际中的应用．
练习册系列答案
名校课堂系列答案
相关题目
3．设方程log2x-（$\frac{1}{2}$）x=0，log${\;}_{\frac{1}{2}}$x-（$\frac{1}{2}$）x=0的根分别为x1、x2，则（ ）
| A． | x1x2=1 | B． | 0＜x1x2＜1 | C． | 1＜x1x2＜2 | D． | x1x2≥2 |
如图是半径为1的半圆，且PQRS是半圆的内接矩形，设∠SOP=α，则其值为$\frac{π}{4}$时，矩形的面积最大，最大面积为1．
7．已知x，y满足不等式组$\left\{\begin{array}{l}{x≤2}\\{y≤3}\\{x+y≥2}\end{array}\right.$．则z=2x+y的取值范围为（ ）
| A． | [-1，3] | B． | [1，7] | C． | [1，3] | D． | [1，5] |