题目内容
如图,A、B是单位圆O上的动点,C是圆与x轴正半轴的交点,设∠COA=α.(1)当点A的坐标为
 时,求sinα的值;
时,求sinα的值;(2)若
 ,且当点A、B在圆上沿逆时针方向移动时,总有
,且当点A、B在圆上沿逆时针方向移动时,总有 ,试求BC的取值范围.
,试求BC的取值范围.
【答案】分析:(1)根据所给的点的坐标计算角的三角函数值,注意所给的点的特点,本题是一个在单位圆上的点,那么,角的三角函数值就可以直接在坐标上体现.
(2)根据边的旋转得到角的大小,应用余弦定理表示出要求最值的量,整理变化用三角函数表示,根据所给的角的范围,写出要求的量的范围,得到结果.
解答:解:(1)∵A点的坐标为 ,
,
根据三角函数定义可知 ,
, ,r=1,
,r=1,
∴ .
.
(2)∵ ,∠COA=α,
,∠COA=α,
∴ .
.
由余弦定理得BC2=OC2+OB2-2OC•OBcos∠BOC= .
.
∵ ,
,
∴ ,
,
∴ .
.
于是 ,
,
即 ,
,
即 .
.
∴BC的取值范围是 .
.
点评:本题是一个解三角形的问题,题目用到余弦定理表示边长,用余弦定理求解三角形的边和角,题目运算量较大,是一个综合问题,可以作为高考题的一问出现.
(2)根据边的旋转得到角的大小,应用余弦定理表示出要求最值的量,整理变化用三角函数表示,根据所给的角的范围,写出要求的量的范围,得到结果.
解答:解:(1)∵A点的坐标为
 ,
,根据三角函数定义可知
 ,
, ,r=1,
,r=1,∴
 .
.(2)∵
 ,∠COA=α,
,∠COA=α,∴
 .
.由余弦定理得BC2=OC2+OB2-2OC•OBcos∠BOC=
 .
.∵
 ,
,∴
 ,
,∴
 .
.于是
 ,
,即
 ,
,即
 .
.∴BC的取值范围是
 .
.点评:本题是一个解三角形的问题,题目用到余弦定理表示边长,用余弦定理求解三角形的边和角,题目运算量较大,是一个综合问题,可以作为高考题的一问出现.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
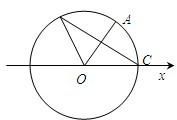 如图,A、B是单位圆O上的动点,C是圆与x轴正半轴的交点,设∠COA=α.
如图,A、B是单位圆O上的动点,C是圆与x轴正半轴的交点,设∠COA=α.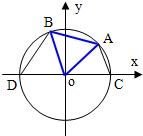 如图,A、B是单位圆O上的点,C、D分别是圆O与x轴的两个交点,△ABO为正三角形.
如图,A、B是单位圆O上的点,C、D分别是圆O与x轴的两个交点,△ABO为正三角形.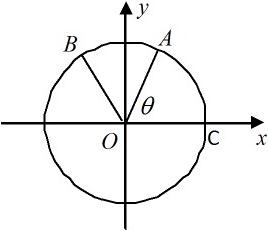 如图:A、B是单位圆上的动点,C是单位圆与x轴正半轴的交点,
如图:A、B是单位圆上的动点,C是单位圆与x轴正半轴的交点,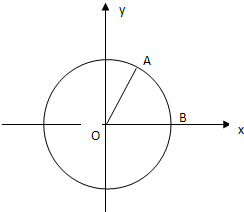 如图,A,B是单位圆上的两个质点,B点坐标为(1,0),∠BOA=60°,质点A以1弧度/秒的角速度按逆时针方向在单位圆上运动;质点B以1弧度/秒的角速度按顺时针方向在单位圆上运动,过点A作AA1⊥y轴于A1,过点B作BB1⊥y轴于B1.
如图,A,B是单位圆上的两个质点,B点坐标为(1,0),∠BOA=60°,质点A以1弧度/秒的角速度按逆时针方向在单位圆上运动;质点B以1弧度/秒的角速度按顺时针方向在单位圆上运动,过点A作AA1⊥y轴于A1,过点B作BB1⊥y轴于B1.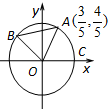 如图,A、B是单位圆O上的点,C是圆O与x轴正半轴的交点,点A的坐标为
如图,A、B是单位圆O上的点,C是圆O与x轴正半轴的交点,点A的坐标为