题目内容
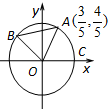 如图,A、B是单位圆O上的点,C是圆O与x轴正半轴的交点,点A的坐标为(
如图,A、B是单位圆O上的点,C是圆O与x轴正半轴的交点,点A的坐标为(| 3 |
| 5 |
| 4 |
| 5 |
-
| 4 |
| 5 |
-
.| 4 |
| 5 |
分析:由三角形AOB为直角三角形,得到∠BOA为直角,根据A坐标求出tan∠AOC的值,进而确定出sin∠AOC与cos∠AOC的值,所求式子中的角度变形后,利用两角和与差的余弦函数公式化简,将各自的值代入计算即可求出值.
解答:解:(1)∵△ABO为直角三角形,
∴∠BOA=90°,
∵点A的坐标为(
,
),
∴tan∠AOC=
,
∴sin∠AOC=
,cos∠AOC=
,
∴cos∠BOC=cos(∠AOC+90°)=-sin∠AOC=-
.
故答案为:-
.
∴∠BOA=90°,
∵点A的坐标为(
| 3 |
| 5 |
| 4 |
| 5 |
∴tan∠AOC=
| 4 |
| 3 |
∴sin∠AOC=
| 4 |
| 5 |
| 3 |
| 5 |
∴cos∠BOC=cos(∠AOC+90°)=-sin∠AOC=-
| 4 |
| 5 |
故答案为:-
| 4 |
| 5 |
点评:此题考查了两角和与差的正弦函数公式,以及任意角的三角函数定义,熟练掌握公式是解本题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 如图,A、B是单位圆O上的动点,C是圆与x轴正半轴的交点,设∠COA=α.
如图,A、B是单位圆O上的动点,C是圆与x轴正半轴的交点,设∠COA=α. 如图,A、B是单位圆O上的点,C、D分别是圆O与x轴的两个交点,△ABO为正三角形.
如图,A、B是单位圆O上的点,C、D分别是圆O与x轴的两个交点,△ABO为正三角形. 如图:A、B是单位圆上的动点,C是单位圆与x轴正半轴的交点,
如图:A、B是单位圆上的动点,C是单位圆与x轴正半轴的交点,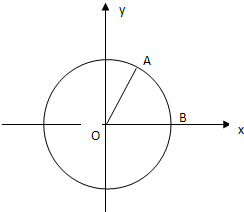 如图,A,B是单位圆上的两个质点,B点坐标为(1,0),∠BOA=60°,质点A以1弧度/秒的角速度按逆时针方向在单位圆上运动;质点B以1弧度/秒的角速度按顺时针方向在单位圆上运动,过点A作AA1⊥y轴于A1,过点B作BB1⊥y轴于B1.
如图,A,B是单位圆上的两个质点,B点坐标为(1,0),∠BOA=60°,质点A以1弧度/秒的角速度按逆时针方向在单位圆上运动;质点B以1弧度/秒的角速度按顺时针方向在单位圆上运动,过点A作AA1⊥y轴于A1,过点B作BB1⊥y轴于B1.