题目内容
在平行六面体ABCD-A1B1C1D1中,已知AB=AD=2a,AA1=a,又知∠A1AD=∠DAB=∠A1AB= .
.
(1)求证:AA1⊥截面B1D1C;
(2)求对角面A1ACC1的面积.
答案:
解析:
解析:
|
(1)如图,∵B1C1=AD=2a C1C=A1A=a ∠B1C1C=∠A1AD=
∴在△B1C1C中,由余弦定理得B1C2=3a2,再由勾股定理的逆定理得C1C⊥B1C,同理可证C1C⊥CD1. ∴C1C⊥平面B1D1C 又C1C∥A1A ∴A1A⊥平面B1D1C (2)∵AB=AD ∵ 作A1O⊥平面AC于O,由∠A1AD=∠A1AB ∴O∈AC 作A1M⊥AB于M,连OM,则OM⊥AB. 在Rt△A1AM中,AM=A1A·cos 在Rt△AOM中,AO=AM·sec 在Rt△A1AO中,A1O= 又在△ABC中,由余弦定理知AC= ∴S |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图,在平行六面体ABCD-A1B1C1D1中,O为AC与BD的交点,若
=
,
=
,
=
,则向量
等于( )
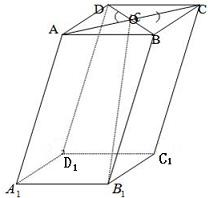
| A1B1 |
| a |
| A1D1 |
| b |
| AA1 |
| c |
| B1O |

A、
| ||||||||||
B、
| ||||||||||
C、-
| ||||||||||
D、-
|
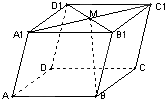 如图:在平行六面体ABCD-A1B1C1D1中,M为A1C1与B1D1的交点.若
如图:在平行六面体ABCD-A1B1C1D1中,M为A1C1与B1D1的交点.若| AB |
| a |
| AD |
| b |
| AA1 |
| c |
| BM |
A、-
| ||||||||||
B、
| ||||||||||
C、-
| ||||||||||
D、
|


 ABCD为菱形,AC为∠BAD的平分线.
ABCD为菱形,AC为∠BAD的平分线.
 =
=



 已知在平行六面体ABCD-A1B1C1D1中,AB=AD=AA1=1,且∠BAD=∠BAA1=∠DAA1=60°,求AC1的长.
已知在平行六面体ABCD-A1B1C1D1中,AB=AD=AA1=1,且∠BAD=∠BAA1=∠DAA1=60°,求AC1的长.