题目内容
已知点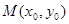 在圆
在圆 上运动,
上运动, ,点
,点 为线段MN的中点.
为线段MN的中点.
(1)求点 的轨迹方程;
的轨迹方程;
(2)求点 到直线
到直线 的距离的最大值和最小值..
的距离的最大值和最小值..
(1)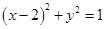 ; (2)最大值为
; (2)最大值为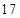 ,最小值为
,最小值为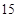 .
.
解析试题分析:(1) 相关点法:因为点 为线段MN的中点,根据中点坐标公式,可分别用
为线段MN的中点,根据中点坐标公式,可分别用 表示
表示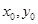 然后代入方程
然后代入方程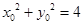 即可得到
即可得到 的轨迹方程;
的轨迹方程;
(2)由(1)的结果,到 的轨迹是圆,利用圆心到直线的距离判断直线与圆的位置关系,并进一步确定圆上的点到直线的距离的最值.
的轨迹是圆,利用圆心到直线的距离判断直线与圆的位置关系,并进一步确定圆上的点到直线的距离的最值.
试题解析: (1)∵点P(x,y)是MN的中点,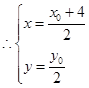 故
故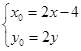
将用x,y表示的x0,y0代入到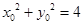 中得
中得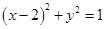 .此式即为所求轨迹方程.
.此式即为所求轨迹方程.
(2)由(1)知点P的轨迹是以Q(2,0)为圆心,以1为半径的圆.
点Q到直线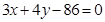 的距离
的距离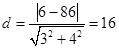 .
.
故点P到直线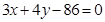 的距离的最大值为16+1=17,最小值为16-1=15.
的距离的最大值为16+1=17,最小值为16-1=15.
考点:1、相关点法求动点的轨迹方程;2、点到直线的距离公式;3、直线与圆的位置关系.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 上,且过点
上,且过点 、
、 .
. 引切线,切点为Q.试探究:
引切线,切点为Q.试探究: 为定值?若存在,求出点R的坐标;若不存在,请说
为定值?若存在,求出点R的坐标;若不存在,请说 ,求直线MQ的方程.
,求直线MQ的方程. 中,已知点
中,已知点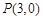 在圆
在圆 内,动直线
内,动直线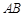 过点
过点 且交圆
且交圆 于
于 两点,若△ABC的面积的最大值为
两点,若△ABC的面积的最大值为 ,则实数
,则实数 的取值范围为 .
的取值范围为 . 中,直线
中,直线 (
( 为参数)与圆
为参数)与圆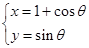 (
( 为参数)相切,切点在第一象限,则实数
为参数)相切,切点在第一象限,则实数 的值为.
的值为. 为圆心的圆经过点
为圆心的圆经过点 和
和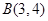 ,且圆心在直线
,且圆心在直线 上.
上. 在圆
在圆 的面积的最大值.
的面积的最大值. 的方程:
的方程: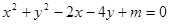 ,其中
,其中 .
. 相交于
相交于 ,
, 两点,且
两点,且 ,求
,求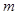 的值;
的值;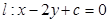 ,使得圆上有四点到直线
,使得圆上有四点到直线 的距离为
的距离为 ,若存在,求出
,若存在,求出 的范围,若不存在,说明理由.
的范围,若不存在,说明理由. 的方程为
的方程为 ,直线
,直线 的方程为
的方程为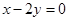 ,点
,点 在直线
在直线 ,切点为
,切点为 .
. ,试求点
,试求点 点的坐标为
点的坐标为 ,过
,过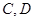 两点,当
两点,当 时,求直线
时,求直线 的方程;
的方程;