题目内容
已知以点 为圆心的圆经过点
为圆心的圆经过点 和
和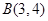 ,且圆心在直线
,且圆心在直线 上.
上.
(1)求圆 的方程;
的方程;
(2)设点 在圆
在圆 上,求
上,求 的面积的最大值.
的面积的最大值.
(1)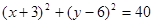 ;(2)
;(2)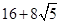 .
.
解析试题分析:(1)圆心 为
为 的垂直平分线和直线
的垂直平分线和直线 的交点,解之可得
的交点,解之可得 的坐标,由距离公式可得半径,进而可得所求圆
的坐标,由距离公式可得半径,进而可得所求圆 的方程;(2)先求得
的方程;(2)先求得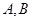 间的距离,然后由点到直线的距离公式求得圆心到
间的距离,然后由点到直线的距离公式求得圆心到 的距离
的距离 ,而
,而 到
到 距离的最大值为
距离的最大值为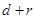 ,从而由面积公式求得
,从而由面积公式求得 面积的最大值.
面积的最大值.
试题解析:(1)依题意所求圆的圆心 为
为 的垂直平分线和直线
的垂直平分线和直线 的交点,
的交点, 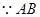 中点为
中点为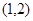 斜率为1,
斜率为1,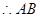 垂直平分线方程为
垂直平分线方程为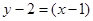 ,即
,即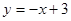 .
.
联立 解得
解得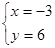 即圆心
即圆心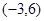 ,半径
,半径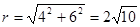 ,
, 所求圆方程为
所求圆方程为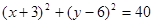 .
.
(2)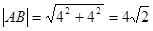 ,
,
圆心到 的距离为
的距离为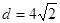 ,
, 到
到 距离的最大值为
距离的最大值为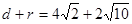 ,
,
所以 面积的最大值为
面积的最大值为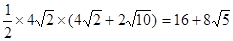 .
.
考点:1、求圆的方程;2、两条直线相交;3、直线与圆相交的性质.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
 过点
过点 ,
,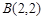 ,并且直线
,并且直线 平分圆的面积.
平分圆的面积. ,且斜率为
,且斜率为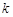 的直线
的直线 与圆
与圆 .
. ,求
,求 )满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为
)满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为
 与曲线C交于两点M、N,若|MN|=4,求直线
与曲线C交于两点M、N,若|MN|=4,求直线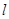 的方程。
的方程。 轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为
轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为 ,若直线l经过点P,且倾斜角为
,若直线l经过点P,且倾斜角为 ,圆C的半径为4.
,圆C的半径为4.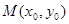 在圆
在圆 上运动,
上运动, ,点
,点 为线段MN的中点.
为线段MN的中点. 的距离的最大值和最小值..
的距离的最大值和最小值..
 时,求直线l的方程;
时,求直线l的方程;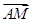 ·
· 是否与直线l的倾斜角有关?若无关,请求出其值;若有关,请说明理由.
是否与直线l的倾斜角有关?若无关,请求出其值;若有关,请说明理由.