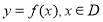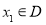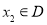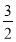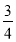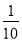Question

已知点动点P满足.

(Ⅰ)若点的轨迹为曲线,求此曲线的方程；

(Ⅱ)若点在直线：上，直线经过点且与曲线有且只有一个公共点，求的最小值．

 

Answer 1

(Ⅰ) ；(Ⅱ)

【解析】

试题分析：(Ⅰ)本题属直接法求轨迹方程，即根据题意列出方程，化简整理即可。(Ⅱ)圆的圆心为半径为，因为直线与圆相切，所以，所以当最小时取得最小值。由分析可知当。

试题解析：【解析】
（Ⅰ）设，由|PA|＝|PB|得

2分

两边平方得 3分

整理得 5分

即 6分

（Ⅱ）当.

,8分

又,10分

.12分

考点：求轨迹方程，点到直线的距离，直线与圆的位置关系。考查数形结合思想、转化思想。